Форма полей напряжений

Как уже обсуждалось, поле напряжений можно получить по структуре, но активные внешние силы не могут быть однозначно определены по полю напряжений. Для разрешения этой проблемы выбирают методы, позволяющие получить геологически допустимые внешние условия, такие как внешние силы или предельные величины напряжения и смещения. Тем самым получают теоретическое распределение напряжений для внутренней части рассматриваемого структурного тела, и можно сравнить теоретически полученные структуры с теми, которые образуются в природе. Поскольку геологическая деформация происходит чрезвычайно медленно, при рассмотрении геологических тел определенного размера и формы обычно можно считать, что всестороннее напряжение на границе раздела и внутреннее напряжение находятся в равновесии. В случаях, когда упругое тело рассматривается в таком состоянии статического равновесия, для определения внутреннего распределения напряжений использовалась функция напряжений Аири. С развитием компьютерной техники обычным методом изучения таких объектов стал метод конечных элементов. Однако в 1950—1960 гг. ведущую роль при механическом анализе геологических структур играли аналитические методы, основанные на функциях напряжения и времени, и поэтому мы хотели бы дать расширенное объяснение этих методов в данной главе. Если читателю нужна более детальная информация, ему следует обратиться к учебникам по теории упругости.

Необходимо удостовериться, что система напряжений, которая может существовать в упругом теле, удовлетворяет нескольким уравнениям теории упругости. Эта задача, однако, решается, если удовлетворяется хотя бы одна функция напряжения.

Для упрощения рассмотрим двухмерную задачу, связанную с состоянием плоского напряжения, действующего в плоскости х—у. В этом случае σ_х, σ_у и τ_ху — единственные компоненты напряжения, действующие на любую точку. Функцию напряжения Φ можно определить следующим образом:


Следовательно, если функция Φ известна, то компоненты напряжения можно получить непосредственно из вышеприведенных определений; возможно также получить главные напряжения σ₁ и σ₂ и угол β, который задает их направления (β — угол между направлением σ_х, σ_у и направлением σ₁, σ₂), и максимальное скалывающее напряжение τ_max из следующих хорошо известных уравнений:



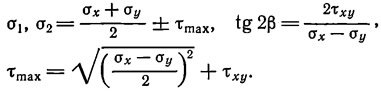
Более того, существуют три важных условия, которым должна удовлетворять функция напряжения: уравнение равновесия напряжений, закон Гука (зависимость деформации от напряжения) и уравнение совместности для деформации. Введение этих условий и преобразование уравнений дает:


Используя оператор Лапласа, это выражение можно записать в упрощенном виде:


В целом решения всех задач, связанных с распределением напряжения в упругом теле, могут быть получены через функцию напряжения Φ, которая удовлетворяет этим бигармоническим уравнениям. На практике функции имеют различные формы, они могут быть многочисленными, экспоненциальными, периодическими и др. Ниже мы приведем несколько примеров их применения к задачам геологического образования разломов.

Поля напряжений и образование разрывов при горизонтальном сжатии

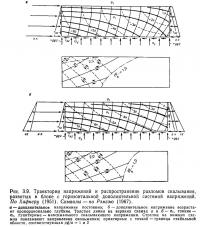
Хафнер (1951) изучал распределение напряжений внутри тел с использованием функций напряжения, приняв различные типы горизонтального напряжения сжатия или скалывания, ожидаемые в земной коре, в качестве граничных условий для этих тел. На основании полученных результатов он предсказал тип и характер разломов в земной коре. Приняв ось z за вертикальное направление, а оси х и у за горизонтальные направления, и, кроме того, полагая, что граничные условия на поверхности Земли выражаются как τ_2x = τ_2y = 0, σ₂ = 0, а вертикальное напряжение за счет перекрытия как σ₂ = —ρg2 (ρ — средняя плотность), он впервые рассмотрел случай, когда поле напряжений в земной коре состоит из гидростатического напряжения и горизонтальных тектонических напряжений, приложенных к ней. Два примера приведены на рис. 3.9, а и б. Первый иллюстрирует случай, когда σ_х = ах—ρg2 (горизонтальное напряжение сжатия равно сумме тектонического напряжения, пропорционального горизонтальному расстоянию, и гидростатического напряжения, пропорционального глубине), σ_z = —ρg2 (вертикальное напряжение равно гидростатическому и пропорционально глубине), а τ_zx = —az (скалывающее напряжение пропорционально глубине). Второй пример иллюстрирует случай, когда тектоническое напряжение ах пропорционально глубине. Линии равного максимального скалывающего напряжения выражаются как множители постоянной а на рис. 3.9, а плоскости трещин скалывания и сдвигов, развивающиеся по ним, вычерчены на основании допущения, что θ = 30°. Величина ρg/a берется в качестве критерия для решения вопроса о том, образуется разрыв или нет; показаны случаи, когда это отношение равно 1 и 2, представляя собой границу стабильной зоны. Это отношение между градиентом давления в вертикальном направлении, обусловленном силой тяжести, и латеральным градиентом приложенного горизонтального напряжения. Как можно судить по рис. 3.9, при величине этого отношения около 2 зона образования надвигов приурочена к небольшим глубинам, но по мере увеличения а зона надвигов смещается глубже. Если вспомнить, что сопряженные надвиги, показанные пунктирными линиями под рисунками 3.9, а и 3.9, б, очень редко встречаются в природе, то этот пример сильно напоминает складчатые зоны, сопровождающие образование однонаправленных шарьяжей, и может применяться при рассмотрении полей напряжений в таких зонах. Хафнер изучил и многие другие случаи.

Поля напряжений и образование разрывов при вертикальном смещении

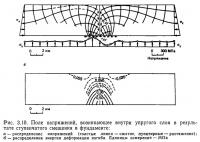
Если Хафнер выразил все граничные условия через напряжение, то Санфорд (1959) проанализировал поля напряжений и разрывы, возникающие в упругом теле, когда основание изотропных однородных упругих тел подвергается вертикальному смещению. Эта модель применима к изучению полей напряжений, возникающих в осадочном чехле в результате вертикального движения фундамента. Поля напряжений, окружающие упругое тело, являются гидростатическими и, так как дополнительное горизонтальное тектоническое напряжение не прилагается, горизонтальное напряжение просто пропорционально глубине. Санфорд изучал эту проблему, использовав функции напряжения, и получил смещение и распределение напряжений. Он проанализировал три типа смещения. Один из них, а именно случай, когда ступенчатое вертикальное смещение возникает у основания перекрывающих толщ благодаря движениям фундамента, разделенного вертикальными сбросами, показан на рис. 3.10, а. Вертикальное смещение на этой диаграмме весьма преувеличено, на самом деле оно не будет превышать 10—12 км в перекрывающей толще длиной 25 км и мощностью 5 км. Следовательно, направление траектории главного напряжения в основном определяется мощностью, а число Пуассона оказывает лишь небольшое влияние.

Санфорд также рассчитал энергию деформации скручивания и установил, что при высоких значениях, вероятно, будет происходить образование разрыва или течение (рис. 3.10, б.).


Как видно из рис. 3.10, а, деформация фактически ограничена областью, расположенной непосредственно над разломом фундамента. Так как поле горизонтального растяжения возникает ближе к относительно приподнятому блоку (левому), то у поверхности в этой области развивается вертикальная трещиноватость или гравитационное разломообразование. Санфорд подтвердил эти результаты экспериментально, использовав для моделирования смеси глины и песка. В итоге он обнаружил, что угол внутреннего трения, равный 28°, лучше всего соответствует теории.

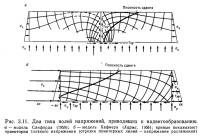
Модели Хафнера и Санфорда, описанные выше, являются основными при любой дискуссии о полях напряжений, возникающей по поводу двух различных факторов, т. е. горизонтального сжатия и вертикального поднятия. Вопрос о том, является ли структурное происхождение Передовых Хребтов Колорадо результатом горизонтального сжатия или вертикального поднятия, был предметом спора в течение 20 лет. Хармс (1965) исследовал поле напряжений в этом регионе, использовав модели Хафнера и Санфорда. Он изучил рои песчаниковых даек кембрийского возраста, внедрившихся в докембрийские породы во время Ларамийской орогении (поздний мел — ранний третичный период), когда развивались Передовые Хребты. Он обнаружил, что в телах, подвергшихся горизонтальному сжатию, сопровождающихся в основном системами вогнутых пологих надвигов, как в первом случае, не было зон, удобных для образования даек. Поднимающиеся тела с системами выпуклых взбросов, как в последнем случае, были благоприятны для образования даек, потому что они сопровождали поле напряжений горизонтального растяжения в относительно приподнятом блоке. Сопоставив это с другими фактами об этом регионе, Хармс сделал заключение, что происхождение Передовых Хребтов связано с вертикальным поднятием (рис. 3.11, а, б).

Наложение полей напряжений

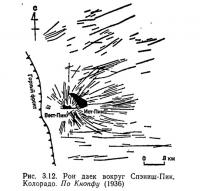
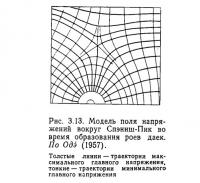
Несколько очень интересных роев радиальных даек обнаружено вокруг Спэниш Пик в Колорадо. Они были изучены Кнопфом (1936) и Джонсоном (1961). Одэ (1957) объяснил, что их распространение и механизм образования обусловлены наложением регионального и локального полей напряжений. Эти рои даек распространены почти симметрично относительно линии, пересекающей Вест Спэниш Пик. Здесь не меньше 500 даек, большинство из них начинается от Вест Спэниш Пик и отклоняется к востоку. Длина некоторых из них превышает 40 км, но на западе дайки очень короткие (рис. 3.12). Большинство даек вертикальны, ширина их обычно составляет около 3 м. В соответствии с теорией Андерсона (1951), дайки развиты вдоль плоскости, перпендикулярной к оси минимального главного напряжения, т. е. к плоскости, содержащей оси максимального и промежуточного главных напряжений. Остается лишь решить, соответствуют ли форма и положение траекторий главных напряжений, рассчитанные на основании приемлемой модели, реальному расположению даек или нет.

Поскольку можно отчетливо представить себе, что во время внедрения даек поле напряжений состояло из локальных сил, обусловленных давлением флюида внутри вулканического центра, и региональных сил, которые, как полагают, были однородны на огромной территории, то симметрия распределения даек означает, что результирующее этих полей напряжений обладало такой же симметрией. Более того, так как можно ожидать, что радиальные дайки с осевой симметрией образуются в результате действия локальных полей напряжений, то можно считать, что симметрия, проявляемая реальными дайками, является отражением регионального поля напряжений, в котором ось максимального главного напряжения была, вероятно, параллельна линии симметрии. Кроме того, отсутствие даек западнее горного фронта показывает, что он образовал жесткий барьер для обоих типов полей напряжений. Следовательно, если упростить задачу, сведя ее к двухмерному пространству, то горизонтальное поле напряжений, существующее в скважинах, подвергающихся гидростатическому давлению и пробуренных по краю неопределенно больших плит, становится моделью локального поля напряжений.

Наконец, при попйтке наложения регионального поля напряжений, полученного по функции напряжения, на локальное,, определенное по аналогичной функции напряжения, получают траектории напряжения, показанные на рис. 3.13; они очень напоминают характер распределения реальных даек.

В каждом из трех приведенных примеров мы предугадали характер образующихся трещин, определяя положение и форму линий главных напряжений. В то же время это позволяет нам оценить происхождение ранее существовавших разрывов.