Межслойные складки в геологических телах

Межслойные складки, подобные изображенным на рис. 5.11, часто наблюдаются в кристаллических сланцах и гнейсах, в которых проявляется хорошо развитая сланцеватость и/или полосчатые текстуры, а также в чередующихся песчаниках и глинистых сланцах и в полосчатых кремнистых сланцах. Межслойные складки характеризуются амплитудами, которые уменьшаются вверх и вниз, как показано на рисунке. Другими словами, складчатые слои постепенно переходят в нескладчатые, и складчатый участок ограничен плоскими слоями (АА' и ВВ' на рис. 5.11). Одна из наиболее существенных особенностей межслойных складок заключается в том, что обычно не отмечается заметной разницы в строении (т. е. минеральном составе или текстуре) слоев между складчатыми и нескладчатыми участками, т. е. складка образуется в системе с однородным строением. Следовательно, нельзя искать причину возникновения этого типа складчатости в различии компетентности между слоем и вмещающей его средой, как в случае однослойных складок.

Происхождение межслойных складок до недавнего времени не затрагивалось. Био (1963) показал, что определенный тип механической анизотропии может послужить причиной, вызывающей складкообразование (теория внутреннего продольного изгиба), и его теория была важным шагом вперед в понимании механизма образования межслойных складок. Начнем с краткого обзора полученных Био теоретических результатов. Рассмотрим форму и распределение деформаций природных межслойных складок, и, наконец, обсудим их происхождение.

Внутренний продольный изгиб анизотропных упругих тел

Био (1963) рассмотрел систему с внутренней слоистостью (например, со сланцеватостью, с чередующимися слоями, имеющими различные механические свойства) под действием начального сжимающего напряжения Р, параллельного напластованию. Принимая координату х параллельной Р, а координату у — перпендикулярной напластованию, он подошел к складкообразованию как к задаче деформации в плоскости х—у. Био предполагал, что под действием начального напряжения Р в системе развивается однородная деформация, и рассматривал бесконечно малую неоднородную деформацию, наложенную на эту однородную начальную деформацию. То есть его основные предпосылки заключаются в том, что складкообразование происходит, когда эта бесконечно малая деформация развивается лишь с незначительными отклонениями, и что характер этой неоднородной деформации определяет форму складки.


Био для упрощения принимал, что материал является несжимаемым, и анализировал деформацию анизотропного упругого тела, для которого связь дифференциальной деформации с напряжением задается уравнением:


где s_xx, s_yy и s_xy дифференциальные напряжения;
e_xx, e_yy и e_xy — дифференциальные деформации;
N и Q — модули упругости, соответствующие чисто сдвиговой (pure-shear) и просто сдвиговой (simple-shear) дифференциальным деформациям, соответственно.

Считается, что механические свойства горной породы неизменны в плоскостях, параллельных слоистости, поэтому уравнение (5.10) не изменяется от выбора оси х в этой плоскости.

Для системы, состоящей из двух правильно чередующихся типов слоев с различными механическими свойствами, уравнение (5.10) дает средние механические свойства системы. Если эти слои механически изотропные и между ними не происходит проскальзывания, то N и Q даются Био как:


где μ₁ и μ₂ — модули упругости для двух типов слоев (μ₁≥μ₂);
α₁ и α₂ — относительные значения мощности слоев (α₁+α₂=1).

Из уравнения (5.11) получаем


Отметим, что если μ₁ и μ₂ не равны, то N больше Q (N > Q), и система в целом ведет себя как механически анизотропное тело. Рассмотрим случай, когда дифференциальные смещения u и v в направлениях х и у выражаются только в виде скалярной функции Φ как



Это поле смещения автоматически удовлетворяет условие несжимаемости. Из теории дифференциальной деформации известно, что Φ удовлетворяет линейному дифференциальному уравнению в частных производных четвертого порядка [9]. Явление внутреннего продольного изгиба тесно связано с тем, что дифференциальное уравнение имеет гиперболическое решение. В этом случае Φ может быть записано следующим образом с использованием некоторой функции φ и реального параметра ξ:


Важным свойством уравнения 5.14 является то, что Φ не изменяется до тех пор, пока (х = ξу) сохраняет некоторую постоянную величину k. Так как дифференциальные смещения определяются исключительно величиной Φ, поле смещений одинаково вдоль линии, заданной (х—ξy) = k. Направление, вдоль которого этот тип деформации не претерпевает изменений, называется «характеристическим направлением» (characteristic direction), наклон которого задается величиной ξ. Био не анализировал динамические аспекты деформации, но физически решение в виде уравнения (5.14) будет соответствовать явлению, когда локальная деформация распространяется вдоль характеристического направления. Био назвал явление, когда однородная деформация превращается в неоднородную по уравнению (5.14), «внутренним продольным изгибом» (internal buckling). Пусть новые модули упругости М и L, включающие в себя начальное напряжение Р, будут определяться выражениями:


Тогда внутренний продольный изгиб произойдет, когда Р достигнет критической величины:



Био различал два типа внутреннего продольного изгиба, и называл внутренний продольный изгиб, удовлетворяющий условиям


«внутренним продольным изгибом первого рода» — internal buckling of the first kind (внутренний продольный изгиб второго рода описан в разделе 5.4). Когда уравнение 5.17 выполняется, Р имеет минимальное значение L при ξ = 0 (рис. 5.12) и, следовательно, ξ = 0 задает наименее стабильное характеристическое направление. Уравнение (5.16) имеет два действительных корня ±ξ при Р=Р₀ > L.

Поле смещения, определяемое уравнением (5.14), полностью зависит от выбора функции φ. Выбор φ, следовательно, необходимо рассматривать для каждой решаемой задачи, а физическое значение ξ изменяется соответственно. Если принять функцию косинуса как частное решение уравнения (5.14), тогда


что при подстановке в уравнение (5.13) дает


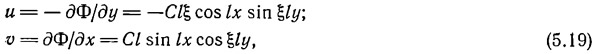
где С — произвольная постоянная, указывающая степень роста складки; l — волновое число в направлении х, равное 2π/L; L — длина волны складки.


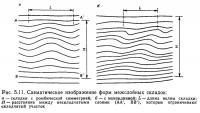
Поле смещения, описываемое уравнением (5.19), определяет геометрию деформированной структуры, аналогичной структуре межслойных складок, которые симметричны относительно их осевой поверхности. Следовательно, теория Био объясняет форму межслойных складок довольно хорошо. Сравнивая поле смещения (уравнение 5.19) с межслойными складками на рис. 5.11, а, получим ξ через длину волны складки L и толщину складчатого участка Н, как


По рисунку 5.12 можно видеть, что чем меньше величина ξ, т. е. чем больше толщина Н по отношению к длине волны L, тем меньше будет начальное сжимающее напряжение Р, необходимое для возникновения внутреннего продольного изгиба.

Внутренний продольный изгиб анизотропных вязких жидкостей

Геологические деформации, происходящие в процессе складкообразования, главным образом, пластичные. Следовательно, вязкие, а не упругие модели будут более реалистичны при моделировании природного складкообразования. Био [9] применил механику жидкостей для расширения приведенной выше теории, чтобы включить в нее внутренний продольный изгиб анизотропных вязких жидкостей. Основные результаты его анализа будут приведены ниже.

Принимая, как и в случае упругой деформации, что материал несжимаем, основное уравнение для анизотропных вязких жидкостей будет записываться в той же форме, что и уравнение (5.10), но N и Q заменяются коэффициентами вязкости η_n и η_t, а компоненты деформации — соответствующими компонентами скорости деформации. Для системы, состоящей из двух типов правильно чередующихся слоев с коэффициентами вязкости η₁ и η₂, уравнения для η_n и η_t идентичны по форме уравнению (5.11) при замене μ₁ и μ₂ на η₁ и η₂, соответственно.

Существуют две принципиальные разницы между упругим и вязким решениями. Во-первых, для возникновения вязкого складкообразования не существует критической нагрузки. Другими словами, складка будет расти независимо от того, насколько мало сжимающее напряжение Р. Во-вторых, хотя квазистатическое упругое решение может предсказать только общую форму складки, при вязком решении анализируется процесс складкообразования.

Вязкие слои, подвергшиеся действию сжимающего напряжения Р, испытывают не только неоднородную деформацию, связанную со складкообразованием, но также и однородное послойное укорочение. Принимая, что АА' и ВВ' (рис. 5.11, а) остаются плоскими в процессе складкообразования, изменения величин L, Н, l и ξ в уравнении (5.19), обусловленные этим однородным укорочением, выражаются как:


где ε_s — среднее укорочение системы, выраженное в виде логарифмической деформации; величины справа представляют собой их исходные значения.

Поле смещения в случае вязкой деформации также может быть записано в форме уравнения (5.19), причем Сl представляет собой максимальную амплитуду складок в системе. Пусть Сl при средней деформации ε_s обозначается через ω, а ее начальное значение — через ш0. Тогда коэффициент усиления ω/ω₀ (показатель, указывающий на степень роста складки) дается приблизительно следующими уравнениями [11] (t в уравнениях Био заменено здесь на ε_s)


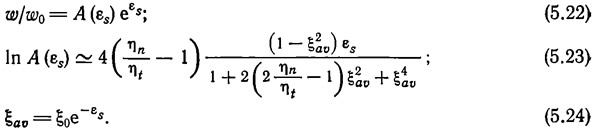
Этот результат показывает, что чем больше отношение вязкостей между двумя типами чередующихся слоев (или, более обычно, чем выше степень механической анизотропии системы) или чем меньше значение ξ₀ (чем больше H₀ по отношению к L₀), тем быстрее будет расти складка (рис. 5.13). Этот вывод не содержит коренных отличий от характеристик упругого решения.

Метод конечных элементов при анализе межслойных складок

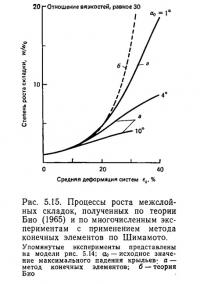
Теория Био может быть дополнена применением к складкообразованию метода конечных элементов, который позволяет с достаточной точностью проанализировать конечную деформацию и распределение напряжений и деформацией в системе. На рис. 5.14 представлен пример межслойных складок в многослойной вязкой жидкости, проанализированный Шимамото (неопуб-ликовано). Коэффициент усиления ω/ω₀ на рис. 5.15 нанесен по отношению к средней деформации системы es при постоянном отношении вязкостей, равном 30, и переменной величине максимального начального падения крыльев α₀. Результат теории Био показан пунктиром, и можно видеть, что его предсказание довольно хорошо согласуется с результатами, полученными методом конечных элементов, когда величина а мала. Как и в случае однослойных складок, сначала складка растет медленно, а затем, после некоторой стадии, ее рост резко ускоряется. Однако, результат для α = 4° показывает, что скорость роста складки начинает уменьшаться, когда максимальное падение крыльев α_max превышает 30—40°. Это противоречит результатам линейной теории Био и означает, что складка не может расти бесконечно.

Направления максимального удлинения (т. е. направления главной оси X эллипсоида деформации) в пределах межслойной складки показаны на рис. 5.14 короткими линиями. Распределение деформаций характеризуется направлениями оси X, проявляющими веерообразное расположение со схождением книзу или кверху в антиклинальных участках компетентных и некомпетентных слоев, соответственно. Уравнение (5.19), выведенное на основании теории Био, позволяет получить только распределение деформаций, усредненное по локальным неоднородным деформациям, обусловленным слоистостью. Следовательно, оно не вполне пригодно для сравнения с природными складками.

Межслойные складки в кристаллических сланцах Самбагава

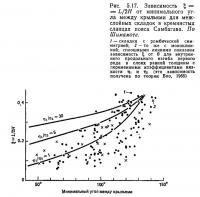
Рассмотрим теперь характеристики природных межслойных складок. На рис. 5.16 показана зависимость длины волны складки L от ограничивающего расстояния Н для межслойных складок в кремнистых сланцах. На этой диаграмме L и H попадают в область, ограниченную пунктирными линиями, а ξ, определяемое по уравнению (5.20), меняется от максимума, равного 0,44 (верхняя линия) до минимума, составляющего 0,05 (нижняя линия). Параметр ξ явно уменьшается по мере роста складок (рис. 5.17).

Существование максимума для ξ можно объяснить на основании теории Био следующим образом. Решение для упругой среды показывает, что под действием начального сжимающего давления ξ₀ будут образовываться лишь складки с ξ меньшим, чем ξ₀ (см. рис. 5.12), и ξ₀ можно отождествить с наблюдаемым максимумом ξ. Решение для вязкой среды показывает, что скорость роста складки резко замедляется, когда ξ превышает 0,3 или близкие значения (рис. 5.13), т. е. складки с ξ, превышающим 0,44, на практике развиваться не могут.

Существование минимума для ξ станет понятным, когда мы рассмотрим, как меняется этот параметр по мере роста складок. Теория внутреннего продольного изгиба Био для вязкой среды предсказывает, что ξ уменьшается в процессе складкообразования в соответствии с уравнением (5.21). Чтобы сравнить его теорию с наблюдаемым изменением ξ, для трех значений отношения вязкостей была рассчитана зависимость параметра ξ от максимального угла между крыльями θ (см. рис. 5.17) с использованием уравнений (5.22) и (5.23). При вычислениях принималось, что начальные значения ξ и θ были 0,45 и 135°, соответственно. Наблюдаемое изменение ξ приблизительно коррелируется с теоретическим прогнозом для η₁/η₂ = 1. Однако, кремнистые сланцы сложены чередующимися слюдистыми и кремнистыми слоями с отношением вязкостей 20—100, судя по их составу и результатам, приведенным в табл. 5.1. Даже учитывая распределение деформаций, которое будет рассмотрено ниже, никоим образом нельзя рассчитать, что отношение вязкостей составляет только 1. Следовательно, теория Био не может объяснить наблюдаемую зависимость ξ от θ.

Главный источник этого несоответствия, возможно, кроется в теоретическом допущении, что АА' и ВВ' на рис. 5.11, а остаются нескладчатыми в процессе складкообразования. Исключая особый случай, когда система сверху и снизу ограничена очень мощными изотропными компетентными слоями, это допущение, возможно, необоснованно. Более вероятно, что плоские слои, контактирующие со складчатым участком, по мере развития складкообразования становятся складчатыми, и, если это так, становится понятным, что наблюдаемая величина ξ намного меньше, чем предсказанная Био. Если в действительности складчатый участок в процессе складкообразования расширяется в направлении, перпендикулярном слоистости, ограничивающее расстояние Н увеличивается, а параметр ξ уменьшается быстрее, чем показывает уравнение (5.21). Так как скорость роста складки больше для меньшей величины ξ (см. рис. 5.13), складкообразование будет ускоряться при расширении складчатого участка. Складчатый участок не может расширяться бесконечно, потому что соседние складчатые участки также будут стремиться расширяться. Минимальное значение для ξ устанавливается, вероятно, взаимодействием между соседними складками.

При складкообразовании в одном слое, заключенном в изотропную среду, влияние складкообразования передается через нее на расстояние, не превышающее длину волны складки (см. раздел 5.5). В противоположность этому, многие межслойные складки имеют Н в десять раз превышающее L (см. рис. 5.16). Вспомните, что направление, перпендикулярное к слоистости, т. е. направление, соответствующее ξ = 0, является наиболее нестабильным характеристичным направлением при внутреннем продольном изгибе первого рода. Следовательно, можно интерпретировать расширение складчатого участка вверх и вниз как распространение локальной деформации, связанной со складкообразованием вдоль этого характеристичного направления. Однако, до сих пор не разработано никакой теории, чтобы можно было предсказать, как складчатый участок расширяется в процессе межслойного складкообразования.

Другая отмеченная особенность межслойных складок заключается в том, что в отличие от однослойных складок, у них нет доминирующей длины волны. Однако, сопротивление изгибу каждого компетентного слоя выше для меньших длин волн, поэтому длина волны складки не может стать бесконечно малой. Как рассмотрено в разделе 5.8, огромные складки, длина волны которых превышает несколько десятков километров, не образуются из-за стабилизирующего эффекта силы тяжести. По-видимому, исходная неупорядоченность слоев присутствует в различных масштабах, поэтому складки, соответственно, будут характеризоваться разными длинами волн, за исключением указанных выше двух крайних значений.

Формы сланцеватости (или кливажа) в межслойных складках, развитых в кремнистых сланцах, в основном те же, что и наблюдаемые в однослойных складках (ср. рис. 5.18 и рис. 5.6), и довольно хорошо согласуются с результатами, полученными с помощью метода конечных элементов (рис. 5.14).

Таким образом, особенности природных складок удовлетворительно объясняются механической моделью Био, и можно заключить, что наиболее важным причинным фактором при межслойном складкообразовании является механическая анизотропия горных пород в целом.