Определение фигуры Земли и аномалий массы по возмущениям орбит искусственных спутников

Фигура Земли

Впервые мысль о том, что Земля представляет собой шар, высказал греческий философ и математик Пифагор еще в VI веке до нашей эры. В III веке до нашей эры Эратосфен оценил ее размеры. В 1617 г. Снелл нашел, что длина градуса меридиана равна 69 милям (111 км). Несколько точнее ее определили Норвуд в 1636 г. и Пикар в 1671 г. Представление о Земле как о шаре сохранялось до тех пор, пока в 1671 г. Рихер не обнаружил, что период колебаний маятника меняется с широтой. Ньютон объяснил этот факт, исходя из постулата, что гравитирующая планета, вращаясь вокруг собственной оси, должна принять форму сжатого сфероида. Однако при измерениях дуги меридиана к северу и к югу от Парижа Кассини получил для северной части дуги меньшую длину градуса, чем для южной. Так как геодезические измерения относятся к углу между нормалями к поверхности эллипсоида, а не между геоцентрическими радиусами-векторами, то результаты Кассини указывали на вытянутость эллипсоида. Таким образом, выводы английских и французских ученых оказались противоречивыми. Чтобы разрешить это противоречие, Французская академия наук в 1735 и 1736 гг. послала экспедиции в Перу и Лапландию для измерения длины градуса меридиана вблизи экватора и около полярного круга. В результате оказалось, что длина градуса меридиана непрерывно возрастает от экватора к полюсу. Это окончательно доказало, что Земля имеет форму сжатого сфероида. Несколько позже Клеро [2] опубликовал свою классическую работу о фигуре Земли, в которой он дал основы математического аппарата для вычисления действительной фигуры Земли и фигуры Земли, находящейся в гидростатическом равновесии.

Методы получения информации о фигуре Земли можно разделить на две группы: геометрические и динамические.

Геометрические методы. Эти методы можно разбить на две категории: наземные и околоземные. К наземным относятся геодезические триангуляционные, трилатерационные и профильные методы. Триангуляция начинается с определения со всей возможной точностью длин и азимутов разумно выбранных базисных линий, которые далее служат опорными для построения всей сети треугольников, покрывающих интересующую нас площадь. Трилатерация похожа на триангуляцию, но отличается тем, что вместо углов здесь измеряются расстояния. Для точного определения фигуры Земли триангуляционными сетями пришлось бы покрыть огромные территории размером с материк и даже более. Однако точность результатов в этом случае была бы невелика. Это объясняется накоплением ошибок, трудностью введения поправок за рельеф, определенных путем измерения высот как функций углов возвышения, а также необходимостью знать точные высоты геоида относительно сфероида. Кроме того, эти методы дороги и занимают много времени; ими трудно, а иногда и невозможно пользоваться, так как трасса измерений должна пересекать национальные границы, топографические препятствия и океаны.


Эти трудности можно преодолеть, воспользовавшись околоземными геометрическими методами с применением искусственных спутников Земли. Одновременные замеры расстояний до спутника или углов, под которыми он виден на нескольких станциях слежения, определяют относительное расположение этих станций, разделенных межконтинентальными расстояниями. Геодезическую связь между любой парой таких станций можно получить с помощью метода вычислений большой дуги. В таком варианте спутник используется в качестве неизвестной точки наблюдения. Если орбита спутника определена достаточно точно, то им можно пользоваться как движущейся точкой наблюдения, положение которой представляет собой известную функцию времени. Тогда величины углов или расстояний будут определять местоположение каждой станции, выраженное в тех же геодезических характеристиках. Надобность в одновременных наблюдениях на других следящих станциях при этом отпадает. Полученные таким образом результаты дают прямую информацию о фигуре Земли.

Динамические методы. Эти методы заключаются в том, что информацию о фигуре Земли получают из результатов измерения силы тяжести на ее поверхности и из данных о константе прецессии, из значений коэффициентов разложения геопотенциала по сферическим функциям, определенных по спутникам, и скорости вращения Земли. С помощью этой информации осуществляется контроль результатов геометрических методов; она же определяет геоид — эквипотенциальную поверхность, знать которую необходимо при расчетах триангуляционных сетей, а также для установления ориентации эллипсоида относимости. С помощью этих же методов можно получить сведения о равновесной фигуре Земли, а следовательно, рассмотреть вопрос о том, находится ли Земля в гидростатическом равновесии. Последнее особенно важно с геофизической точки зрения, так как при вычислениях аномалий силы тяжести равновесная фигура Земли является наилучшей поверхностью относимости. В этом случае полученные аномалии будут прямо указывать на существование в земной коре и верхней мантии негидростатических полей напряжений.


Для определения с помощью описываемых методов действительного сжатия Земли нам нужно знать величину коэффициента геопотенциала J₀. (J = 3J₂/2, где J₂ — коэффициент второй гармоники в разложении геопотенциала по сферическим функциям. В настоящей работе J для гидростатически уравновешенной Земли мы обозначаем через J_h, а для реальной — через J₀. Там, где различие невозможно или необязательно, мы будем просто пользоваться символом J.) До запусков искусственных спутников Земли точное определение J₀ было невозможно. Поэтому все попытки сводились к тому, чтобы найти способ достаточно надежной оценки J₀. Большинство исследователей принимали при этом, что Земля находится в состоянии гидростатического равновесия, т. е. J₀ = J_h. В этом случае величину J₀ находили с помощью теории Клеро [2], которая в 1885 г. была несколько упрощена Радо. Прежде чем перейти к дальнейшему изложению, приведем основные положения этой теории.

Теория Клеро. Рассмотрим внешний потенциал тела, симметричного относительно экваториальной плоскости и относительно оси, перпендикулярной этой плоскости. Будем считать, что поверхность тела является эквипотенциальной поверхностью. В этом случае [5, 15, 13, 21]


откуда

Из уравнения (1) или (2) можно получить f₀, если известно J₀ (т считается известным), и наоборот.


Условие гидростатического равновесия можно записать аналитически в виде дифференциального уравнения:


где Ψ — потенциал силы тяжести, р — давление в данной точке внутри тела и ρ — плотность в этой же точке. Отсюда следует, что р должно быть функцией Ψ, а ρ —либо константой, либо также функцией Ψ. Так как эквипотенциальные поверхности задаются условием Ψ = const, то на этих поверхностях р и ρ также должны принимать постоянные значения. Это с очевидностью следует из уравнения (3). Таким образом, условие гидростатического равновесия для внутренних частей Земли заключается в допущении, что эквипотенциальные поверхности являются также и поверхностями равной плотности. Рассмотрим потенциал во внутренней точке тела, симметричного относительно экваториальной плоскости и перпендикулярной ей оси. Вводя условие гидростатического равновесия, получим два граничных условия, которые совместно задают форму внешней поверхности Земли, находящейся в гидростатическом равновесии. Эти граничные условия имеют следующий вид [21]:


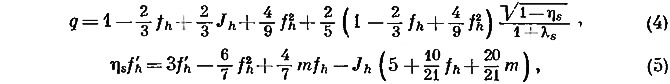
где

С — момент инерции Земли по отношению к полярному диаметру, A — момент инерции Земли по отношению к экваториальному диаметру, М — масса Земли, а_е — ее экваториальный радиус, m = (ω²r²_m/GM, ω — угловая скорость вращения Земли, r_m — средний радиус Земли при sin²φ = 1/3, где φ — широта, G — константа гравитации, η_s — значение на поверхности Земли параметра η, который зависит от распределения плотности внутри Земли, λ_s — значение на поверхности Земли параметра λ, который указывает на отклонение от единицы некоторой функции F(η), введенной Радо в гидростатическую теорию.



Совместное решение уравнений (4) и (5) приводит к явному выражению [19. 21] f_h, а именно:


где

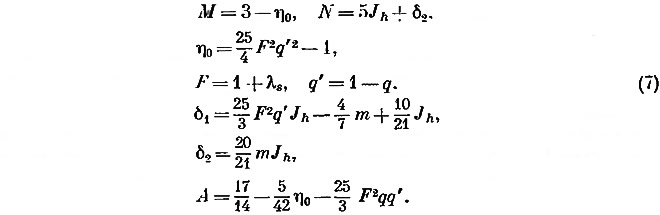
Уравнение (6) определяет f_h, если известны J_h, m и λ_s.

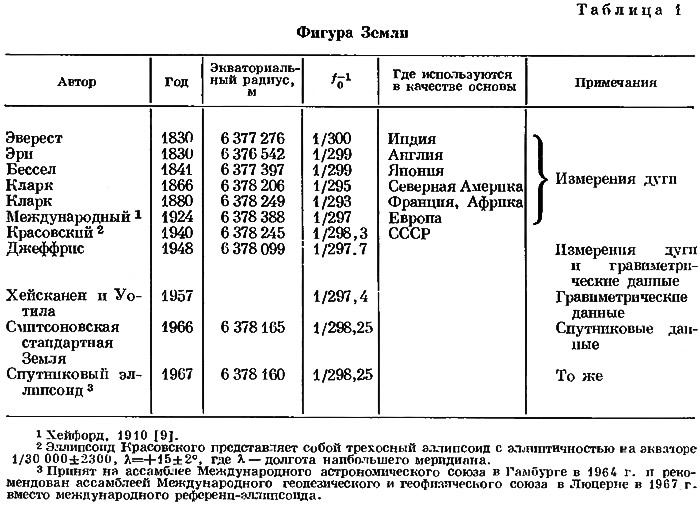
Действительная фигура Земли. Если J₀ известно, то величину сжатия f₀ для действительной Земли можно получить из уравнений (1) и (2). Так, для J₀ = 1623,969·10^-6, определенного по спутникам [23], f₀ = 1/298,25 ±0,05. В 1967 г. эта величина сжатия и была рекомендована к использованию Международным геодезическим и геофизическим союзом взамен принятой ранее величины 1/297,0 (сжатие международного референц-эллипсоида). Одновременные исследования орбит спутников показали, что значение коэффициента J₃ при третьей степени зональной гармоники заключено в пределах от —2·10^-6 до —3·10^-6. Отличие от нуля этого коэффициента объясняется тем, что со стороны южного полюса Земля «приплюснута» несколько сильнее, чем со стороны северного полюса (так называемая «грушевидная» форма). Те же исследования показали, что не равен нулю и коэффициент J₂₂ при второй степени секториальной гармоники второго порядка, связанный с эллиптичностью экватора. Однако, судя по современным данным, этой эллиптичностью можно пренебречь. В табл. 1 приведены некоторые результаты изучения действительной фигуры Земли, полученные в различное время с помощью геометрических и динамических методов.

Фигура равновесия Земли. В доспутниковую эпоху точное значение коэффициента J₀ не было известно, поэтому для нахождения наилучшей аппроксимации для формы Земли использовался метод Клеро, в котором считается, что Земля находится в гидростатическом равновесии. Де Ситтер [5] слегка изменил формулы Дарвина [4] для теории Клеро, развитой до второго порядка, заменив в них экваториальный радиус средним радиусом Земли. Его уравнения можно получить, исключив с помощью уравнения (1) коэффициент J_h (де Ситтер не делает различия между J₀ и J_h), появляющийся в правой части уравнений (4) и (5). Уравнения де Ситтера запишутся в следующем виде:


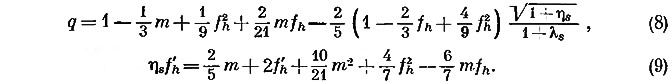
Метод де Ситтера [5, 6], которому следовал и Буллард 11], заключался в оценке q на основе гидростатической теории с использованием данных о распределении плотности внутри Земли; вычислении J из соотношения J = qH (H известно) и затем нахождении сжатия из уравнения (1). Подробное обсуждение этого метода можно найти в работах де Ситтера [5], Булларда [1], Джонса [15] и Кана [19, 21]. Результаты, полученные с помощью этого метода различными исследователями, приведены в табл. 2.

Когда при помощи спутников удалось определить величину J₀, появилась возможность независимого вычисления f₀ и f_h. Большинство исследователей [11, 25, 18] для определения гидростатического сжатия пользовались уравнениями де Ситтера (8) и (9). Полагая, что λ_s = 0, они получали значение % из уравнения (8), подставляли это значение в уравнение (9) и получающееся в результате квадратное уравнение решали относительно Д. Джеффрис [14] предложил великолепный способ вычисления поправок к членам второго порядка при помощи численного интегрирования, избавляющий от необходимости применять уравнения де Ситтера. Этот метод ясно обрисовал всю проблему в целом, но в нем аналитический вид получен лишь для членов первого порядка. В табл. 2 приведены результаты различных исследователей. Они показывают, что гидростатическое сжатие Земли меньше действительного. Однако возникли некоторые сомнения относительно правильности решения, полученного с помощью гидростатической теории, развитой де Ситтером. Было высказано предположение, что в решении, основанном на этой теории, f_h получается из решения той части «гидростатических уравнений», где не используется ни одно из соотношений, выведенных на основе теории внешнего потенциала, таких, например, как уравнения (1) и (2). Однако Кан [19] показал, что в процессе вывода уравнений (8) и (9), чтобы избавиться от J_h в их правых частях, де Ситтер пользовался уравнением (1). Но из-за того, что это было проделано в самом начале вывода этих уравнений, факт использования уравнения (1) потерял свою очевидность, что, по-видимому, и привело в дальнейшем к путанице. Кан модифицировал уравнения де Ситтера (5), восстановив J_h, и получил измененные гидростатические уравнения в виде уравнений (4) и (5), или, что предпочтительнее, в форме одного гидростатического уравнения (6). Так как в правой части этих измененных уравнений теперь появляется J_h и поскольку для получения решения, имеющего геофизический смысл, J_h следует рассматривать как еще одно неизвестное, система уравнений (4) и (5) становится неполной и требуется еще одно граничное условие. Это условие и было найдено Каном [20] в работе, где в общих чертах сформулирован корректный подход к решению проблемы гидростатического равновесия. Это решение в сокращенном виде приводится ниже.

При выводе уравнений (1) и (2) не делалось никаких предположений об условиях, существующих в глубинах Земли. Следовательно, эти уравнения справедливы как для случая гидростатического равновесия, так и для условий негидростатических. Для случая негидростатических условий они связывают между собой J₀ и f₀, а для случая гидростатического равновесия — J_h и f_h. Отсюда уравнения (1) и (2) можно написать в следующем виде (m считается известным):


для негидростатического случая и

для гидростатического случая.

Гидростатическое уравнение (6) можно записать в виде


Принимая во внимание, что на поверхности Земли в случае гидростатического равновесия уравнения (11) и (12) должны совпадать, получим


Это уравнение дает общее решение проблемы гидростатического равновесия. Частные численные решения уравнения (13) зависят от того, какие параметры будут приняты известными при решении гидростатического уравнения. Так, если считать, что полярный момент инерции гидростатической модели равен действительному (т. е. вычисленному по наблюденным величинам J и H), то f_h = 1/299,75 + 0,05 (λ_s = 0). Это значение близко к полученному О’Кифом [25], Хенриксеном [11], Джеффрисом |14] и Каном [18], но структура решения несколько иная [20, 21], чем у указанных выше исследователей. Если допустить, что динамическое сжатие Н гидростатической Земли равно наблюденному для реальной Земли [20, 21], решение уравнения (13) дает f^-1_h = 297,29 + 0,05 (λ_s = 0). Эта величина такая же, как у Булларда [1], но использованный здесь метод проще. Такова гидростатическая модель доспутниковых времен. Третье решение уравнения (13) можно получить [20, 21], взяв величину J, определенную по спутникам, за исходную. Сжатие гидростатической фигуры в этом случае оказывается равным действительному для реальной Земли. Однако в двух последних случаях полярный момент инерции для гидростатической модели получается больше реального. Это приводит к серьезным осложнениям с динамикой. В табл. 3 приведены суммарные результаты, полученные при таком решении. По мнению Ледерштегера [24], если бы Земля находилась в равновесии, она имела бы большую скорость вращения вокруг оси (звездные сутки составляли бы 23 час. 44 мин. 25,4 сек.) и большее сжатие — около 1/295,8. Вначале, когда Земля была жидкой, степень сжатия могла находиться в соответствии с уменьшающейся центробежной силой. В процессе отвердевания это соответствие нарушилось. Изменение формы твердой Земли начало запаздывать, что и привело к небольшому отклонению от состояния равновесия. Только водная оболочка могла следовать за уменьшением скорости вращения и последовательно пришла к современному сжатию, равному 1/298,3, тогда как у твердой поверхности сжатие равно 1/295,8.

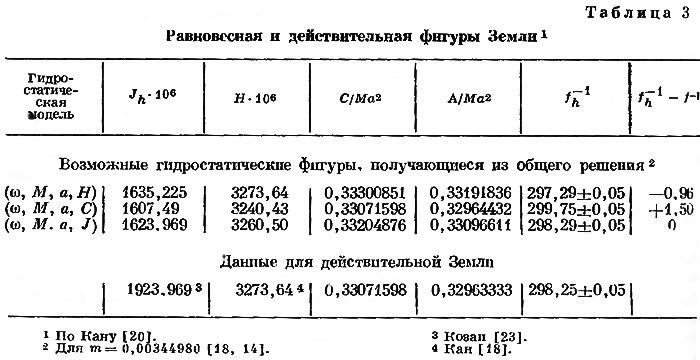
У гидростатической модели, имеющей геофизический смысл, гидростатическое сжатие должно составлять около 1/299,75 ±0,05, т. е. соответствовать сжатию, которое получается при условии, что момент инерции гидростатической модели такой же, как и у реальной Земли.

Аномалии массы, обнаруженные по возмущениям орбит спутников

Если бы Земля была идеальным шаром, ее гравитационный потенциал V можно было бы записать в виде


Спутник двигался бы вокруг такой Земли, подчиняясь законам Кеплера, т. е. по замкнутой эллиптической траектории, с Землей в одном из фокусов этого эллипса и центром масс, лежащим в его плоскости. Однако потенциал реальной Земли отличается от потенциала строго сферического тела на некоторую небольшую величину R, которая называется возмущающим потенциалом. Поэтому потенциал для действительной Земли запишется в виде


Из-за этого возмущающего потенциала на спутник действуют малые возмущающие силы. Так как R мал по сравнению с потенциалом притяжения сферы GM/r, то орбиты спутников еще можно считать эллиптическими, но характеристики этих эллипсов будут теперь медленно изменяться во времени. Такое изменение любого из элементов орбиты обычно называют «возмущением» этого элемента.

Возмущающий потенциал можно выразить через сферические гармоники:


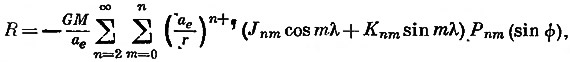
где P_nm — присоединенные1 функции Лежандра. Для m = 0 их обычно записывают в виде P_n(sin φ) и называют полиномами Лежандра. Функции cos mλP_nm(sin φ) и sin mλP_nm(sin φ) суть поверхностные сферические гармоники. Для m = 0 они называются зональными гармониками. При m ≠ 0 их называют тессеральными гармониками. J_nm и K_nm — постоянные коэффициенты перед различными сферическими гармониками в разложении R. Влияние возмущающего потенциала R на различные орбитальные характеристики спутников выражается следующими уравнениями:


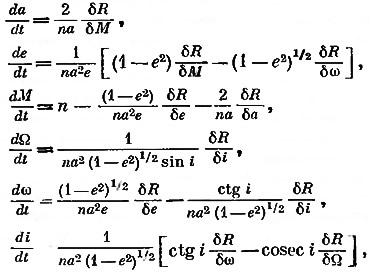
где Ω — прямое восхождение восходящего угла, а — большая полуось орбиты спутника, n — среднее движение, определяемое соотношением GM = n²a³, е — эксцентриситет, ω — угловое расстояние перигея, i — наклон орбиты и М — средняя аномалия, определяемая как М = n(t—τт), где τ — время прохождения спутника через перигей.

Влияние зональных гармоник на орбиту спутника намного сильнее, чем тессеральных, которые определяют вариации, зависящие от долготы. Зональные гармоники вызывают вековые и длиннопериодные изменения прямого восхождения угла Ω и углового расстояния перигея со и только длиннопериодные изменения эксцентриситета и наклонения орбиты i. Длиннопериодные изменения за счет нечетных зональных гармоник сильнее выражены в е и i, в то время как вековые изменения, вызываемые четными зональными гармониками, заметнее в Ω и ω. Это упрощает определение зональных гармоник. Тессеральные гармоники, вызывающие короткопериодные изменения орбитальных элементов, определить намного труднее. Для этого требуется увеличить количество наблюдений и распределить их более равномерно в пространстве и во времени. Но, наблюдая за этими изменениями, можно, по крайней мере в принципе, определить и тессеральные гармоники. Из-за возникающих трудностей определения коэффициентов при гармониках для проверки надежности их определения предпринимались многочисленные попытки сравнить их величины, полученные по различным спутникам, с величинами, вычисленными по результатам гравитационной съемки на поверхности Земли. В настоящее время считается, что низкие гармоники определены с достаточной точностью. К значениям же зональных и тессеральных гармоник более высоких порядков, полученным с помощью спутниковой информации, следует относиться с осторожностью.

В этих гармонических коэффициентах заложена информация об аномалиях масс, которые выражаются обычно либо в терминах гравитационных аномалий, либо в ундуляциях геоида. Ундуляции геоида и гравитационные аномалии вычисляются по отношению к некоторой поверхности относимости. Для геофизических исследований малого масштаба эту поверхность относимости можно выбирать достаточно произвольно, но при глобальных исследованиях она должна быть унифицированной. Обычно в качестве поверхности относимости выбирается международный референц-эллипсоид (см. табл. 1). В 1967 г. Международный геодезический и геофизический союз рекомендовал для использования «спутниковый» эллипсоид, параметры которого определены на основе уточненной информации, обеспеченной искусственными спутниками Земли. Однако для оценки действительных крупных аномалий масс, связанных с корой и верхней мантией, и для последующего геофизического изучения этих аномалий наилучшей поверхностью относимости будет фигура Земли, находящаяся в равновесии. В этом случае отклонения от нее наверняка указывают на существование гидростатических напряжений в Земле и особенно в коре и верхней мантии. Отклонение действительной фигуры Земли от ее равновесной формы дает, кроме того, возможность оценить величину минимальной прочности, которой должна обладать Земля, чтобы выдерживать эти гидростатические напряжения. При локальных исследованиях эти напряжения можно не учитывать, но в масштабе всей Земли они становятся весьма существенными. Поскольку результаты изучения гравитационного поля по спутниковым данным точнее отражают длиннопериодные компоненты поля, то особенно важно, чтобы аномалии, получаемые с помощью спутников, рассчитывались по отношению к равновесной фигуре, с тем чтобы максимально полно использовать получаемую информацию. В случае выбора какой-либо другой поверхности относимости в гравитационных аномалиях могут появляться несуществующие длиннопериодные компоненты, амплитуды которых будут зависеть от отклонений выбранной поверхности от равновесной фигуры.

Если f_h известно, то для равновесной фигуры можно вычислить зональные гармонические коэффициенты J₂₀ и J₄₀ (их обычно записывают в виде J₂ и J₄) из уравнения (1) и уравнения


Эти два коэффициента определяют равновесную фигуру с достаточной степенью точности.

Ундуляция геоида. Ундуляцию геоида N в точке (r, φ, λ) можно получить из уравнения


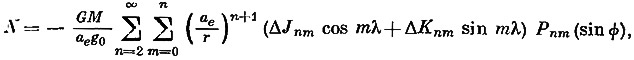
где ΔJ_nm = J_nm наблюденное — J_nm для поверхности относимости, ΔK_nm = K_nm наблюденное — K_nm для поверхности относимости; g₀ — теоретическая сила тяжести на референц-эллипсоиде в точке (r, φ, λ). В нашем случае для поверхности относимости единственными отличными от нуля J_nm будут коэффициенты J₂₀ и J₄₀. Следовательно, за исключением этих двух коэффициентов, все другие коэффициенты ΔJ_nm и ΔK_nm будут равны наблюденным J_nm и K_nm.

Гравитационные аномалии. Гравитационную аномалию Δg в точке (r, φ, λ) получим из уравнения


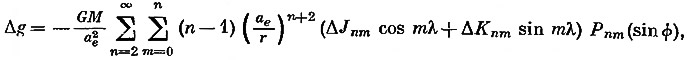
где ΔJ_nm и ΔK_nm определены выше.

Минимальная прочность Земли. Джеффрис [13, 14] определил разности напряжений, возникающие за счет отклонения Земли от состояния гидростатического равновесия. В основном они обусловлены неравенством величин Р₂, т. е. отличием второго коэффициента в разложении действительного потенциала по сферическим функциям от второго коэффициента в разложении потенциала для гидростатической модели. В предположении, что напряжения, обусловленные различием Р₂, выдерживаются за счет прочности: 1) всей Земли до ядра и 2) только до глубины 0,1 радиуса, получим для равновесной фигуры с f^-1_h = 299,75 два значения прочности:


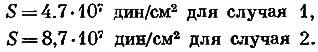
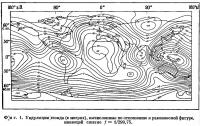
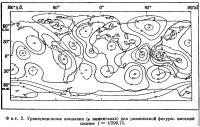
Гравитационное поле. На фиг. 1 изображены ундуляции геоида, а на фиг. 2 — гравитационные аномалии, вычисленные по отношению к эллипсоиду со сжатием 1/299,75. Эти ундуляции и аномалии получены из зональных гармонических коэффициентов Козаи [23] и тессеральных гармонических коэффициентов Гапошкина [7]. Результаты изучения гравитационного поля по спутниковым данным дают общее представление об этом поле в глобальном масштабе. Представление гравитационного поля в виде сферических функций сделано лишь до гармоник восьмого порядка. Таким образом, гравитационные аномалии на фиг. 2 можно сравнить с аномалиями, полученными с помощью наземной съемки и осредненными по площадям размером 22,5X22,5°. В таком масштабе адекватно отражаются лишь длиннопериодные компоненты. Короткопериодные компоненты гравитационных аномалий, наиболее интересные для геофизиков, здесь представлены слабо [22]. Это еще более очевидно, если сравнить дисперсию гравитационного поля, определенную по спутникам, с дисперсией аномалий в свободном воздухе, полученных с помощью наземной гравитационной съемки. Если через Δg обозначить аномалию силы тяжести в любой точке поля, то дисперсия поля запишется в виде


Var (Δg) для аномалий гравитационного поля, определенного по спутникам, составляет 145 мгл (var (Δg) равна 136 мгл для того же поля, рассчитанного по отношению1 к международному референц-эллипсоиду и составляет 119 мгл для поля, отнесенного к эллипсоиду со сжатием, равным 1/298,25), в то время как для аномального гравитационного поля (аномалии в свободном воздухе), полученного с помощью наземной съемки, дисперсия составляет 1201 мгл [16]. Полученное по спутникам гравитационное поле Земли при той степени детализации, которая здесь рассматривается, позволяет выявить лишь большие по площади региональные аномалии, такие, как большая положительная аномалия к юго-юго-западу от побережья Исландии, две отрицательные аномалии к западу и востоку от южной части Северной Америки, отрицательная аномалия в Индийском океане вблизи Цейлона и очень ярко выраженные положительные аномалии в районе Соломоновых островов и Новой Гвинеи.

Геофизический смысл этих аномалий пока не совсем ясен. Учитывая длиннопериодность аномалий, можно допустить, что они связаны либо с аномальными массами, расположенными достаточно глубоко, либо с интегральным эффектом большого числа аномальных масс, расположенных в коре и верхней мантии. В любом из этих случаев какой-то вклад в аномалии будет вносить поверхностная топография. Правда, рельеф создает эффект лишь второго порядка малости, и корреляция между планетарными аномалиями гравитационного поля и рельефом оказывается низкой (на это указывал Джеффрис [13]). Лучшее представление о взаимоотношении гравитационного поля и топографии можно получить с помощью анализа энергетических спектров [17] гравитационного поля, полученного по спутниковым данным, и глобальных вариаций топографии. Такой анализ был выполнен для значений степенной дисперсии рассматриваемых здесь функций. Если J_nm и K_nm — полностью нормализованные постоянные коэффициенты в разложении по сферическим гармоникам функции на сферической поверхности, то степенная дисперсия D²_n определяется в виде


Коэффициент корреляции ρ_n любых двух функций, скажем гравитационных аномалий Δg и топографии Т, равен


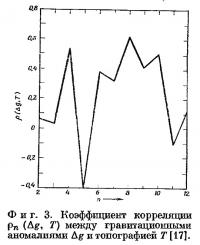
где D²_n (Δg) — дисперсия Δg, D²_n (Т) — дисперсия Т и D²_n (Δg, Т) — совместная дисперсия Δg и Т. График зависимости коэффициента корреляции от степени гармоники п приведен на фиг. 3. Корреляция довольно неопределенна для n≤5. Для 6≤n≤10 она более систематична. Для n > 10 корреляция между гравитационным полем и топографией снова становится незначительной.

На фиг. 4 приведены энергетические спектры трех вариантов аномального гравитационного поля. Так как вертикальные шкалы на графике для каждой кривой различны, разности по вертикали между этими кривыми не могут служить линейной мерой действительных различий в интенсивности рассматриваемых полей. Наиболее важной особенностью фиг. 4 является то, что спектральная кривая В проходит между спектральными кривыми А и С. Это можно интерпретировать таким образом: поскольку изостазия имеет место на всех длинах волн [17], следовательно, значительная часть гравитационных аномалий создается факторами, приуроченными к верхней мантии Земли.

Для некоторых аномальных районов на основе имеющейся геофизической информации довольно трудно создать какую-то смысловую схему. Некоторые из таких районов, например район положительной аномалии над Срединноатлантическим хребтом, аномальны и в других отношениях: пониженные скорости упругих волн в верхней мантии, сильные магнитные аномалии, высокий тепловой поток в срединной части хребта и пониженный на его склонах. Гравитационное поле хорошо согласуется здесь с региональным топографическим рельефом; аномалии Буге показывают,что рельеф скомпенсирован. Трудно увязать все эти факты, если не допустить, что пониженные значения скоростей в верхней мантии указывают на повышенную плотность или что существует еще не открытая слоистость в верхней мантии. Уорзел [30] предложил три модели возможного теоретического распределения масс (все в верхней тридцатикилометровой толще), которые объясняют гравитационное поле Срединноатлантического хребта. Кук [3] предположил, что пониженные скорости в мантии обусловлены перемешиванием корового и мантийного материала в результате конвекции с сопутствующим ей повышенным тепловым потоком. Однако такие предположения, вполне разумные для Срединноатлантического хребта, не объясняют соотношений, наблюдаемых в районе Индийского океана, где с помощью спутников обнаружена широкая отрицательная аномалия. Она приурочена к стабильному океаническому бассейну, расположенному между узким вулканическим хребтом и поднятием типа Срединноатлантического хребта, многие геофизические особенности которого сходны с отмеченными для Срединноатлантического хребта.

Именно это несоответствие между гравитационным полем и другими геофизическими характеристиками в региональном масштабе порождает сомнения в правильности интерпретации и указывает на необходимость более детальных геофизических исследований территорий с аномальным гравитационным полем. Отрицательная гравитационная аномалия в Индийском океане, чуть южнее острова Цейлон, и положительная аномалия в районе Соломоновых островов — два региона, наиболее интересные для детального геофизического изучения; на это указывает характер связи поверхностной геологии с тектоническим строением этих регионов.