Плотность и состав верхней мантии

В настоящей статье рассматриваются некоторые вопросы, связанные с проблемой определения плотности и состава верхней мантии. Для этой цели из геофизических исследований наиболее полезными являются измерения гравитационного поля Земли, времени пробега и амплитуды различных сейсмических волн, а также периодов свободных колебаний Земли. Исследования верхней мантии и переходной зоны невозможно отделить от изучения Земли в целом. Величины различных интегралов по всей массе Земли ограничиваются такими важными значениями, как средняя плотность и момент инерции или периоды низкочастотных гармоник. С другой стороны, не существует общих решений, которые бы в той или иной степени пе зависели от более пли менее произвольных предположений относительно некоторых свойств, поскольку при отсутствии таких допущений невозможно определить плотности и распределение скоростей сейсмических воли. Даже в нулевом приближении, выражая все величины в зависимости от одного только радиуса, мы имеем неограниченное число степеней свободы при ограниченном количестве наблюдений. Однако положение становится доступным контролю, если предположить существование непрерывности в пределах некоторых определенных зон, связывая прерывистость в распределении плотности с прерывистостью в значениях скоростей сейсмических волн и вводя некоторые физические или математические гипотезы, касающиеся степени изменения радиуса. Накопление экспериментальных данных по поведению известных веществ при соответствующих температурах и давлениях позволило пересмотреть некоторые из этих предположений и отбросить те из них, которые с физической точки зрения оказались неприемлемыми.

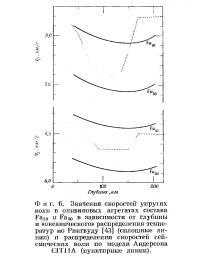
Модели строения внутренних частей Земли, основанные на сейсмологических данных, фактически не изменявшиеся на протяжении тридцати лет. в настоящее время подверглись серьезному пересмотру, особенно в вопросах прерывистости в распределении скоростей и градиентов скоростей, которые являются наиболее существенными при физической интерпретации данных. Многие модели описаны в работах Андерсона [2, 4] и Калои [20]. Быстрый прогресс исследований в области экспериментальной петрологии привел к важным изменениям ряда классических представлений; эти изменения рассмотрены в работах Кларка и Рингвуда [24] и Рингвуда [43] при обсуждении данных о составе мантии.


Региональные исследования позволяют выявить различия в строении верхней мантии не только между океанами и континентами, по и в пределах этих структурных единиц. Поскольку многие проблемы еще находятся в стадии изучения, представляется наиболее целесообразным рассмотреть лишь несколько общих вопросов, связанных с интерпретацией полученных данных, независимо от принятой модели сейсмической структуры. Ввиду неопределенности значений скоростей, характеризующих «слой пониженных скоростей», физико-петрологическое решение, согласующееся с сейсмическими данными, но не определяемое ими, может оказаться в конце концов наиболее удовлетворительным. Наши рассуждения относятся в основном к верхним 200 км мантии. Ниже (по разным гипотезам на различных глубинах) наблюдается более или менее быстрое возрастание сейсмических скоростей с глубиной, что объясняется переходом кристаллических структур в более плотные модификации. О характере последних мы можем теперь судить на основании данных экспериментальной минералогии и исследований по ударному сжатию горных пород при высоких давлениях. Эта переходная область в настоящей статье не рассматривается.

Для более полного ознакомления с этим вопросом читателю можно рекомендовать недавно опубликованную монографию «Мантия Земли» под редакцией Гэскелла [26].

Вначале будет рассмотрено влияние температуры и давления на величины скоростей и плотности в самом верхнем двухсоткилометровом слое мантии. Автор предполагает при этом, что в первом приближении по своим упругим свойствам этот слой эквивалентен оливину. Предполагается, что по составу верхняя мантия соответствует некоторым разновидностям перидотита, основным компонентом которого является оливин. Акцессорные минералы, к числу которых относится ромбический пироксен, характеризуются упругими свойствами, очень близкими к свойствам оливина. Небольшие количества гранатов и шпинели, вероятно, обеспечивают более высокие скорости, а полевых шпатов и амфиболов — более низкие скорости. Отправным пунктом при рассмотрении более сложных перидотитов являются расчеты, выполненные для представляющего типичный состав агрегата, состоящего из оливина (т. е. дунита).


Начиная с Боуэна [17], происхождение базальта объясняли процессом частичного плавления перидотита. Ряд авторов высказывали предположение, что некоторые объемы расплава могли сохраняться в течение продолжительных периодов времени в виде капелек или ячеек, распределенных в нерасплавленном остатке. Состав последнего меняется в зависимости от количества расплава, но близок к составу оливина. Таким образом, при построении модели упругости частично расплавленного перидотита можно основываться на свойствах оливина и базальтового стекла. Это не совсем точно соответствует химизму, но вполне допустимо для начального обзора возможностей предлагаемой модели.

Наконец, автор кратко рассмотрит вопрос о вычислении плотности непосредственно по значениям скоростей.


Р и S используются здесь как для обозначения давления и энтропии в различных производных, так и для обозначения двух различных скоростей сейсмических воли. Такие обозначения являются общепринятыми. Полностью однозначные обозначения, видимо, трудно ввести, если только не отвергнуть обычные символы.

Упругие свойства оливина

В работах, опубликованных за последнее время, содержится большое количество экспериментальных данных но упругим свойствам оливина. Однако источник, который давал бы всю необходимую информацию, до сих пор отсутствует. Кроме того, в различных опытах использовались различные вещества. Верма [63] определил динамические упругие константы монокристалла оливина (перидота), представляющего собой драгоценный камень. Берч [11—13], Симмонс [50], Канамори и Мидзутани [33], а также Кристенсен [23] исследовали дуниты в условиях давлений до 10 кбар. При этом меньше всего изменился дунит Твин-Систерс, для которого полученные величины довольно хорошо согласуются с величиной, рассчитанной для агрегата оливина, изучавшегося Верма и характеризующегося таким же отношением Mg/Fe. Шрейбер и Андерсон [47] определили пьезокоэффициенты, а также некоторые другие свойства синтетического образца поликристаллического форстерита, пористость которого составляла 6%. Сога и Андерсон [55] установили зависимость скорости сейсмических воли от температуры. Они основывались на измерениях, проведенных при температуре до 1000° К, и экстраполировали данные для пористого форстерита в область температур до 2500° К. Величины V_S для дунита при температурах до 500° С и давлении 9 кбар были получены Берчем [14]. Мак-Куин и др. [39] и Трунин с соавторами [61] опубликовали результаты измерений ударного сжатия различных дунитов. Их измерения не соответствуют тем давлениям, которые существуют в верхней мантии, но важны для понимания состояния переходного слоя и нижней мантии.


Существует несколько методов расчета упругих постоянных квазиизотропных однородных агрегатов на основании упругих постоянных монокристаллов. Хилл [32] показал, что два классических метода Фойгта и Реусса позволяют получить верхний и нижний пределы величин К и g (величины, определенные по этим методам, обозначены в табл. 1 как V и R соответственно). Величина сжимаемости агрегата, полученная по методу Реусса, точно соответствует сжимаемости монокристалла. Оба предела, ограничивающие величину G, различаются между собой всего на 4%, а скорости, вычисленные по средним значениям Реусса, которые будут использованы в дальнейших рассуждениях, равны 8,40 и 4,90 км/с соответственно. Эти значения хорошо согласуются с известными величинами для дунита в том случае, когда мы сопоставляем скорости не при нулевом давлении (поскольку пористость уменьшает величину скорости), а при давлении 10 кбар, почти полностью исключающем влияние пористости. Параметры для искусственного пористого форстерита отклоняются в ожидаемом направлении, т. е. величины плотности, скоростей сейсмических волн и модулей значительно ниже, чем для плотного вещества.


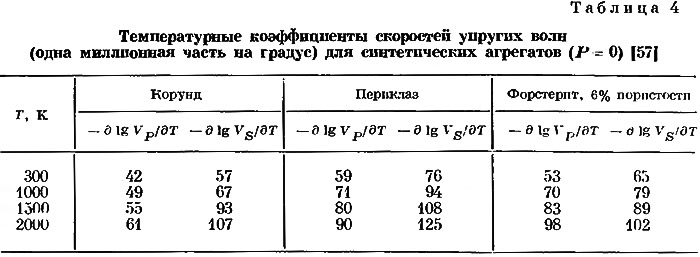
Уравнения, выведенные Сога и Андерсоном [55], позволяют вычислить для искусственного форстерита скорости как функцию температуры. Из этих данных мы можем получить температурные коэффициенты, а также величины скоростей в сравнении со скоростью при комнатной температуре. Ниже приведены данные для форстерита, а также для периклаза и корунда, которые представлены синтетическими агрегатами с нулевой пористостью.

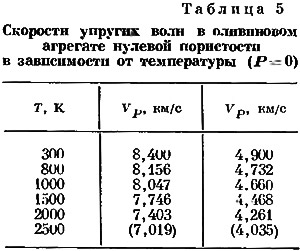
Анализ табл. 2, 3 и 4 позволяет высказать следующие замечания. В пределах одного и того же температурного интервала до 500° С изменения значений V_S для дунита и искусственного форстерита почти одинаковы. Пористость оказывает, очевидно, небольшое влияние на относительное изменение скоростей в этом интервале температур. Изменения значений скоростей в периклазе и форстерите до температур около 2000 К почти одинаковы. По мере возрастания температуры все коэффициенты по абсолютной величине увеличиваются. Для форстерита по сравнению с двумя другими веществами коэффициенты для V_P и V_S значительно ближе по абсолютной величине. Мы не будем обсуждать вопрос о том. в какой степени некоторые из этих результатов зависят от специальных предположений и выбора определенных данных. Предполагается, что относительные величины, приведенные для агрегата форстерита в табл. 2, можно применить к значениям скоростей для плотного агрегата в табл. 1. Полученные в результате такого сопоставления величины скоростей см. в табл. 5.





Для того чтобы выяснить влияние, оказываемое давлением, автор использует данные Адамса [1] по сжимаемости дунита до давления 12 кбар и данные Бриджмена [18] по сжимаемости перидота из Красного моря до давления 40 кбар. Измерения Бриджмена свидетельствуют о почти линейном изменении объема с изменением давления, хотя можно использовать квадратичную зависимость, которая дает К_T=1,22 мбар и не очень определенную величину dK/dP≈2. Адамс получил величину средней сжимаемости, равную 0,79 мбар^-1, или К_T=1,26 мбар, что хороню согласуется с динамической величиной (табл. 1). Шрейбер и Андерсон [47] исследовали влияние давления до 2 кбар на сейсмические скорости в пористом агрегате форстерита; их данные приведены в табл. 6. Измерения скоростей в горных породах можно также использовать при определении пьезокооффициентов. Данные Берча, Симмонса и Кристенсена для дунита Твин-Систерс, полученные при давлениях несколько килобар, могут быть представлены прямыми линиями, т. е. начальная кривизна, связанная с закрытием пор, устранялась, насколько это было возможно. Эти результаты включены в табл. 6. Здесь наблюдаются некоторые расхождения. Все значения для дунита, приводимые в таблице, примерно одинаковы, но несколько выше, чем для пористого форстерита. Коэффициенты для V_Р и V_S для пористого форстерита отличаются настолько сильно, что кажутся аномальными величинами.


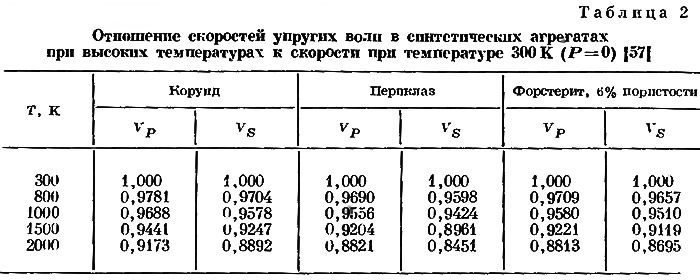
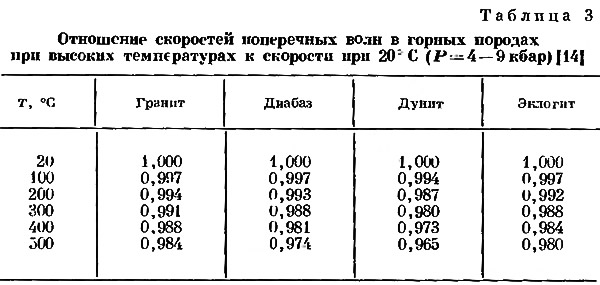
Приблизительные значения этих коэффициентов можно установить несколькими способами. Если принять V_ф=(K/ρ)^1/2, то будем иметь:


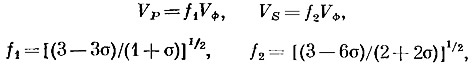
где σ — коэффициент Пуассона. Тогда


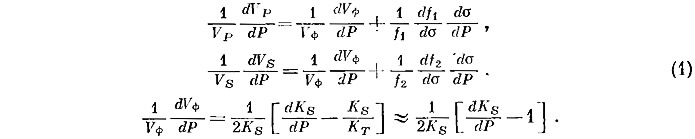
Если вместо производной по Р мы возьмем производную по Т. то в первых двух уравнениях в сущности мы заменяем Р на Т, а третье уравнение будет выглядеть следующим образом:


Теперь df₁/dσ ≈ —1,4 и df₂/dσ ≈ —1,9 в представляющем интерес интервале значений σ. Если σ = 0,25, f₁ = 1,342, f₂ = 0,775 и dK_S/dP = 4, то мы имеем


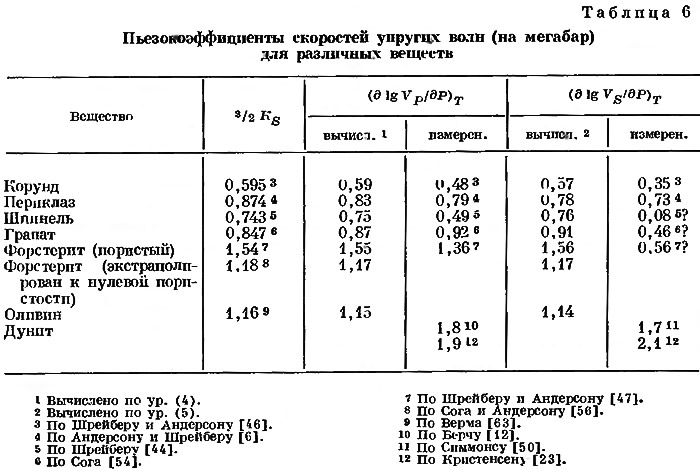
Таким образом, эти два коэффициента будут равны, за исключением члена с dσ/dP, и обратно пропорциональны K_S. Для оливина 3/2 K_S = 1,16 мбар^-1, для пористого форстерита 1,5 мбар^-1. Значения коэффициентов скоростей сейсмических волн, полученные Шрейбером и Андерсоном, приведены в табл. 6, причем dσ/dP = 0,74 мбар^-1. Это значение, по-видимому, аномально высокое. Во всяком случае, такой коэффициент не может применяться достаточно широко, так как в противном случае мы получим невозможные величины для о. Пьезокоэффициенты скоростей, определенные для дунитов, вероятно, являются слишком высокими из-за остаточной пористости; этим же следует объяснять большое различие в величинах коэффициентов V_Р и V_S для пористого форстерита. Значения коэффициентов этих двух скоростей для очень плотных корунда и периклаза почти одинаковы при dσ/dP около 0,1 мбар^-1. Для оливина при dσ/dP = 0,1 мбар^-1 мы получаем


Эти величины основаны на «нормальном» значении (dК_S/dP)_T = 4. Величину 4,8, приводимую Шрейбером и Андерсоном для форстерита, едва ли можно здесь использовать, так как она связана со слишком низкой скоростью изменения V_S. Скорости, определенные для дунита, дают dK/dP≈6. При давлении ниже 400 кбар Мак-Куин, Марш и Фриц получили для дунита величину dК/dР≈2,5. Это значение приблизительно соответствует величине, приводимой Бриджменом для давлений в диапазоне 40 кбар, хотя и не ясно, относится ли эта величина к оливину, не претерпевшему фазовое превращение. Таким образом, неопределенность влияния давления вплоть до 100 кбар составляет 50%. В дальнейших расчетах для обеих скоростей принято значение 1 мбар^-1.

Величины пьезокоэффициентов для квазиизотропных агрегатов, приводимые в работах Андерсона и Шрейбера, основаны на постоянных для монокристаллов. Спи включены в виде относительных величин в табл. 6. Для граната и шпинели значения V_S, по-видимому, очень занижены. Даже при высокой точности измерений изменение давления в 2 кбар слишком мало, а способ нахождения постоянных для агрегатов на основе данных для монокристаллов может привести к ошибке. Хотя, по нашему мнению, величины для V_S будут несколько меньшими, чем для V_P, различия для этих веществ кажутся чрезмерно большими.

Другой метод оценки величин пьезокоэффициентов основан на теории конечных деформаций [19]. Для больших давлений предельные значения определяются из следующих уравнений:


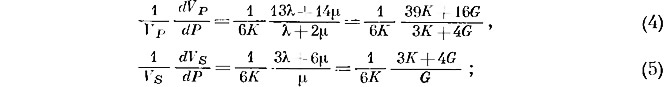
λ и μ в данном случае соответствуют постоянным Ламэ, а μ=G.

Для λ=μ. или σ=0,25, оба коэффициента для V_P и V_S равны 3,2К; отклонение от этой величины увеличивается эквивалентно отклонению σ от величины 1/4. Вновь следует отметить (табл. 6) чрезмерно низкие значения для V_S в случае шпинели, граната и пористого форстерита и высокие значения для природного дунита. Относительно хорошее соответствие наблюдается для V_P. Это свидетельствует о том, что либо подтверждаются проведенные измерения, либо оправдано пренебрежение членом третьего порядка в упругом потенциале.

Основываясь на данных сейсмологии, мы можем грубо оценить dσ/dP. В нижней мантии о увеличивается от 0,276 на глубине около 1000 км до 0,298 на глубине 2400 км, что составляет 0,022 приблизительно на 0,7 мбар. В результате мы получаем величину dσ/dP=0,03 мбар^-1. но на это значение может оказать значительное влияние повышение температуры. Однако можно ожидать, что, подобно многим пьезокоэффициентам, эта величина уменьшится при повышении давления, и в условиях небольших давлений вполне реальным может быть значение 0,1 мбар^-1. Хотя величина dσ/dT, как правило, положительная, можно полагать, что из-за обычно противоположного действия давления и температуры dσ/dP может быть отрицательной величиной.

При высоких температурах (αK_S)^-1(dK_S/dT) почти не зависит от температуры, и для пористого форстерита эта величина составляет —4,1 [56]. Тогда


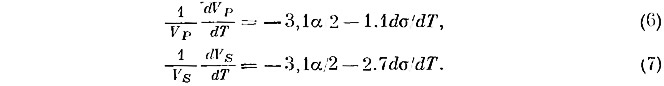
При dσ/dT=10·10^-6 [56] и коэффициенте теплового расширения, определенном Скиннером [53] для оливина с Fa₁₀, мы получим величины, которые в основном согласуются с коэффициентами, выведенными из уравнений Сога, Шрейбера и Андерсона и приведенными в табл. 4.

Плотность оливина в зависимости от температуры и давления до глубин 200 км можно вычислить исходя из коэффициента теплового расширения и модуля объемного сжатия при 1 атм, которые являются функциями температуры, и из уравнения состояния, справедливого вдоль изотермы вплоть до максимального сжатия, составляющего примерно 7%. Скиннер [52] привел функциональную зависимость объема от температуры, основанную на рентгеновском изучении форстерита до температуры 1100°С; предполагается, что формула Скиннера справедлива до температуры 2000°К. Необходимо знать модуль объемного сжатия в том же интервале температур. Он рассчитывается из значений скоростей (табл. 5) с поправкой на разницу между величинами К_S и К_T. Полученные в результате значения несколько меньше тех, которые были рассчитаны с использованием коэффициента (dK_S/dT)_Р=—0,13кбар/°С, приведенного в работе Сога и Андерсона [56] для К_S при комнатной температуре. Однако различие несущественно для наших целей. Для изотерм мы используем уравнение


где у = ρ/ρ₀, а ρ₀ — плотность при температуре Т и Р = 0. Результаты этих расчетов приведены в табл. 7 и 8.



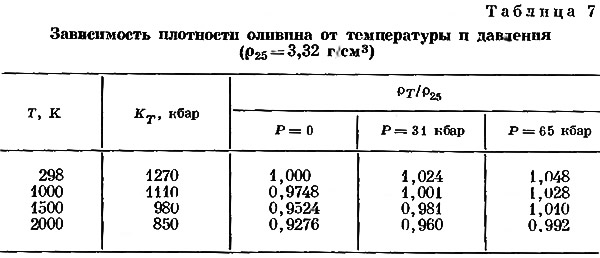
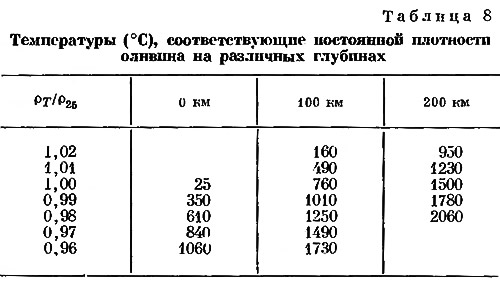
Условия постоянной плотности в плоскости Т—z представлены почти прямыми линиями с наклоном, равным приблизительно 7—8° С/км. Исходя из этого можно вычислить значения плотности изотропного агрегата оливина приблизительного состава Fo₉₀Fa₁₀ для любого распределения температуры, причем ошибка, по-видимому, не будет превышать 1%.

Зона пониженных скоростей: однородный слой

Известно, что с глубиной в пределах большей части мантии скорости сейсмических волн возрастают. Однако еще в 1926 г. Гутенберг предложил объяснять аномалию амплитуд волн на расстояниях около 15° противоположным изменением скоростей. В результате в большинстве схем распределения скоростей сейсмических волн фигурирует «слой пониженных скоростей». При этом существует множество вариантов — их столько же, сколько и сейсмологов (даже еще больше, если учесть числовые модели, рассчитанные вычислительными машинами). Если происходит направленное вниз отражение, то может существовать область, где нет «основания» луча, в связи с чем значения скоростей обычными методами определит], невозможно. Дисперсия поверхностных волн дает нам некоторые указания на распределение скоростей и плотности, но это не означает, что таким путем может быть получено единственное решение. Кроме того, путаницу в эту проблему вносят математические модели, предусматривающие разрывы значений скоростей и плотности. Не всегда ясно, связаны ли эти разрывы с характером вычислений, предполагающих идеализацию более постепенных природных изменений, или они соответствуют физическим разрывам первого рода.

Многое ли можно объяснить, рассматривая изменение температуры и давления в однородном по составу слое? С увеличением глубины z давление возрастает согласно гидростатическому соотношению dP = gρ dz, и мы вправе ожидать увеличения плотности и скорости при возрастании давления. С глубиной увеличивается и температура, а плотность и скорости при возрастании температуры уменьшаются. По-видимому, самая высокая скорость увеличения температуры наблюдается вблизи поверхности; при увеличении глубины она должна уменьшаться. На некоторой глубине влияние температуры компенсирует влияние давления. Следует выделить несколько различных критических градиентов температуры.

Во-первых, соотношение при постоянной плотности в однородной среде, в которой не происходит никаких фазовых изменений. При определении теплового расширения а и несжимаемости К_T можно записать:


Аналогично записывается соотношение для постоянной скорости V(V_P или V_S):


Это соотношение необходимо отличать от соотношения, определяющего критическое отражение, выведенное из условия для направленного отражения на расстоянии радиуса г [29, 19]: dV/dr < V/r. В сфере условие dV/dr = 0 всегда обозначает направленное вверх отражение. Такое условие может быть отождествлено с условием минимума в слое пониженных скоростей. Градиенты, необходимые для направленного вниз отражения (допуская непрерывность всех величин), должны превышать (dT<dz)_крит [10]:


Величиной 1/r иногда пренебрегают при рассмотрении критического градиента, но она является существенной частью числителя.

Эти градиенты для некоторых веществ приведены в табл. 9; радиус r принят равным 6250 км, но не учитывается влияние давления на коэффициенты.


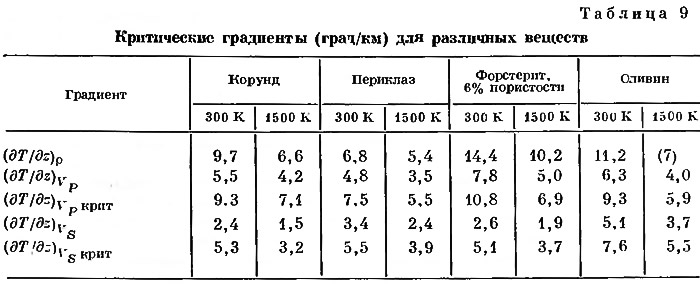
Принимая во внимание ранее выполненные расчеты [10, 62, 37], мы находим, что различные по значениям критические градиенты сопоставимы с величинами геотермических градиентов верхней мантии. Значения критических градиентов для теневой зоны характеризуются большими величинами для V_P, чем для V_S, хотя для оливина это различие невелико и, по-видимому, лишь незначительно отличается от нуля. Для постоянной плотности градиенты, вероятно, мало отличаются от градиентов для критического значения величин отраженных волн V_P в тех случаях, когда учитываются неопределенности.

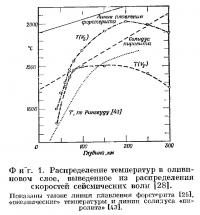
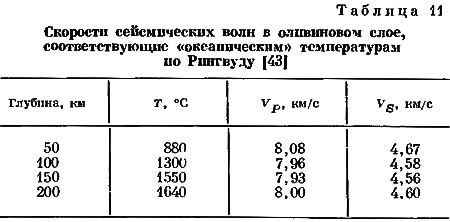
Используя данные для оливина, изложенные в предыдущем разделе, перейдем к рассмотрению следующих вопросов. Каким температурам соответствует известное распределение сейсмических скоростей в верх них 200 км мантии, если считать, что мантия до этих глубин состоит из одного оливина? Каким скоростям сейсмических волн соответствует известное распределение температур? Возьмем в качестве примера распределение скоростей по Гутенбергу [28] и Андерсону [4, модель CIT11A] и распределение «океанических» температур по Рингвуду [43].

Скорости сейсмических волн задаются как функция глубины. Определяя номинальные давления для каждой глубины, мы сначала приводим значения скоростей к нулевому давлению с учетом пьезокоэффициента (см. предыдущий раздел). Поправка, соответствующая глубине 200 км или давлению 65 кбар. составляет около 6% от величин скоростей. По исправленным величинам скоростей определяем соответствующие им температуры (табл. 10) с использованием кривых, построенных по данным табл. 5. Значения скоростей для продольных и поперечных сейсмических волн дают два вида распределения температур, которые будут совпадать в том случае, если сейсмические численные данные (и предполагаемые изменения скорости) не противоречат гипотезе оливпнового состава слоя. Отрицательные градиенты свидетельствуют о том, что мы имеем дело с районами, в которых увеличение скоростей значительно превышает увеличение, связанное с изотермическим сжатием.


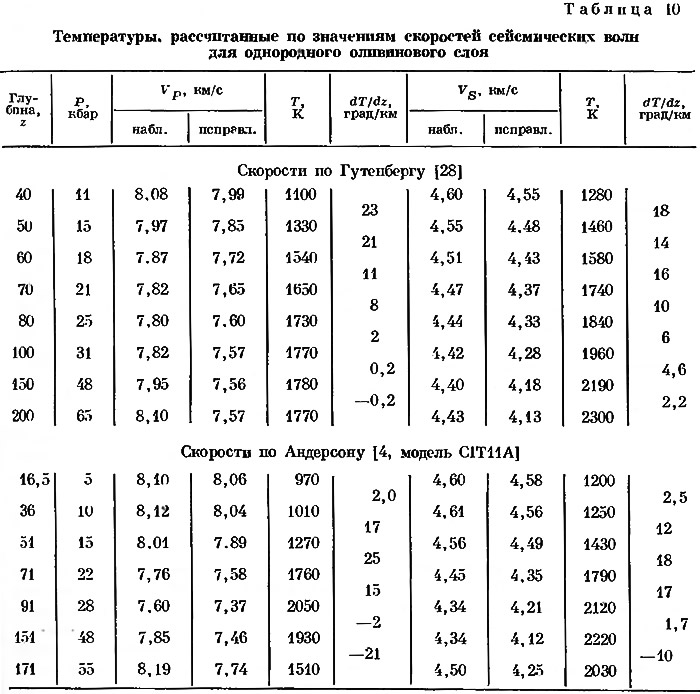
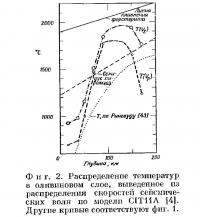
Гутенберг предложил две модели изменения скоростей непосредственно под разделом Мохоровичича. Вначале он писал: «Судя по новым данным, остается мало сомнений в том, что астеносферный слой пониженных скоростей для обоих типов сейсмических волн начинается сразу же под разделом Мохоровичича» [28]. Как отмечали Мак-Дональд и Несс [37], при таком положении возможно обычное распределение температур и существование однородного слоя. При небольшой корректировке значений скоростей можно, очевидно, согласовать гутенберговскую модель распределения скоростей [28] с вероятной кривой распределения температуры и предполагаемой однородностью состава вещества до глубины около 200 км. Для более глубоких зон необходим переход в вещество с более высокими значениями скоростей сейсмических волн. Однако в другом месте Гутенберг пишет: «В океанических областях чаще, чем под континентами, сразу же под границей Мохоровичича может существовать тонкий слой, в котором скорость возрастает с глубиной, прежде чем начнется ее уменьшение» [29, стр. 112]. Эта особенность отражена в модели CIT11A, где увеличение скоростей происходит в интервале глубин от 16 до 36 км; для однородного слоя, состоящего из оливина, градиент составляет только 2° С/км. Если такая деталь в распределении скоростей является существенной, то мы имеем либо аномалию в распределении температур, либо постепенный переход к такому составу, который может компенсировать воздействие нормального градиента температуры. Рингвуд [43] предложил объяснить этот факт дегидратацией амфиболового перидотита; не исключена и десерпентинизация.

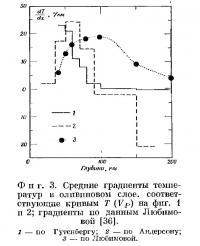
В качестве возможных аномалий температур Любимова [36] приводи распределение температуры, которое в качественной форме напоминает кривые, полученные по модели CIT11A, в их восходящей части. Такое распределение основано на определении изменения величины теплопроводности под действием температуры с учетом уменьшения фононной и повышения радиационной проводимости по мере роста температуры. При этом на глубине около 100 км должна существовать минимальная проводимость, а рассчитанная температура составляет 1400°С; теплопроводность на этой глубине равна 0,002 кал/(с·см·°С). Любимова приводит следующие градиенты:


Однако едва ли проводимость достигает такой малой величины при температуре 1400°С. Последние измерения инфракрасной трансмиссии при повышенных температурах [7] показывают, что только для перидота радиационный вклад при температуре 1240° С составляет 0,005 кал/(с·см·°С). По данным Канамори и др. [34], минимальная проводимость оливина (в направлении 001) наблюдается при температуре 500°С и равна около 0,009 кал/(с·см·°С). Максимальный отрицательный градиент скорости по модели CIT11A соответствует глубине 60 км, а последующее возрастание скоростей не соответствует положительному градиенту температуры в однородном слое. Однако под океанами, где генерирующий тепло слой, вероятно, толще, может существовать менее заметпый максимум температурного градиента.

Абсолютные величины температур зависят от значений скоростей упругих волн в оливине; они меньше для перидотита, содержащего некоторое количество более сжимаемых минералов. Следует вспомнить, что при температурах свыше 1000° К эти скорости получены при линейной экстраполяции К и G. Более высокие температуры, рассчитанные по V_S, по сравнению с температурами, рассчитанными по V_Р, очевидно, связаны с тем, что величины V_S могут быстрее уменьшаться с увеличением температуры, чем это показано в табл. 5. Однако расхождение получается больше для распределения но Гутенбергу, чем при расчете по модели CIT11A. Необходимо незначительно изменить отношения скоростей, чтобы получить совпадение температур до глубины 10и км.

Все рассчитанные температуры ниже кривой плавления форстерита [25], но на глубине свыше 60 км превышают солидус «пиролита» [43]. Температуры, не превышающие солидус пиролита, можно получить, если принять, что скорости равны 8,2 и 4,7 км/с соответственно. Такие значения отвечают предложенному Рингвудом «пироксеновому пиролиту».

Зона пониженных скоростей: частичное плавление

Многие исследователи высказывали предположение о существовании в зоне пониженных скоростей частично расплавленного вещества. Модель полного расплавления не согласуется с приливными деформациями и данными сейсмологии. Наиболее вероятным процессом, обусловливающим образование базальтовых магм из перидотита, представляется частичное плавление. Между началом частичного плавления и уходом магмы базальтовая жидкость могла быть распределена в веществе в виде пленок или капель.

Некоторые аспекты этой гипотезы были рассмотрены Симодзуру и др. [48, 49].

Белоусов [8] изложил их в более конкретной форме; он предположил, что объем жидкого базальта может быть равен ~ 10%, а это должно вызывать уменьшение V_Р в зоне пониженных скоростей на 0,3 км/с и уменьшение плотности на 0,1 г/см³.

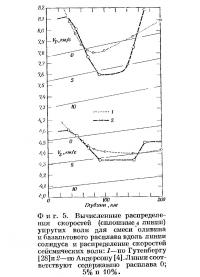
Эти гипотезы могут быть оценены с помощью формул, приводе!тыл в работах Мак-Кензи [38], Олдройда [42] и Хасина [31], для двухкомпонентного вещества, в котором один компонент существует в виде маленьких сферических полостей. Пусть с — объемная доля полостей, заполненных базальтовым расплавом, имеющим нулевую жесткость и модуль объемной сжимаемости стекла K₁. Матрица имеет жесткость G₂, и модуль объемной сжимаемости оливина Кг. Вероятно, для перидотита нужно использовать несколько иные величины, но в любом случае различие между свойствами кристаллического перидотита и расплавленного базальта будет большим и выводы существенно не изменятся. Для вычислений возьмем К₂=1,30 мбар, K₁=0,65 мбар [16], G₂=0.80 мбар, плотность оливина примем равной 3,324 г/см³, а стекла 2,76 г/см³. По Хасину, соотношение для К сложного вещества имеет вид К/К₂=1—с(3—3σ)/(5—7σ), или приближенно 1—0,7 с для соответствующей величины σ. Соотношение для G получено Мак-Кензи и Хасином в очень приблизительном виде: G/G₂=1—2 с. Это справедливо для малых величин с; предположим, что соотношение выполняется для с до 10%. Вычисленные величины К, G и скоростей сейсмических волн приведены в табл. 12 для нормальных температуры и давления. Для нас представляют интерес температуры, достаточные для плавления базальта,— по крайней мере 1200° С. Увеличение температуры до 1200° С приводит к снижению скоростей упругих волн в оливине на 8%. Эту величину мы примем в качестве поправки для грубой оценки величин скоростей упругих воли в сложном веществе при температуре 1200° С (последние две колонки табл. 12). Влияние давления почти не зависит от с, и при давлении 30 кбар скорость V_P увеличивается на 0,3 км/c, a V_S — на половину этой величины. С помощью значений, приведенных в табл. 12, можно получить отношение ΔV/Δρ для членов этих серий. При 1200° С это отношение для V_P составляет 8,2, а для V_S 7,9. что совершенно не совпадает с величинами, полученными для изометрического сжатия, когда ΔV_P/Δρ≈3 и ΔV_S/Δρ≈1,5. Уменьшение плотности на 0,1 г/см³ обусловлено расплавлением 15% вещества и приводит к уменьшению обеих скоростей на 0,8 км/с. Если при таком подходе говорить об уменьшении скоростей на 0,3 км/с, это будет означать, что в расплавленном состоянии должно находиться около 6% вещества, а плотность уменьшится только на 0,03 г/см³, или на 1%. Отношение V_Р/V_S возрастает с увеличением доли расплава. Эти результаты находятся по крайней мере в качественном согласии с выводами Хейлса и Дойла [30], касающимися мантии под западной частью США. Согласно этим авторам, отношение ΔV/Δρ колеблется между 9 и 13, что объясняется «приближением одной из составных частей к расплавленному состоянию». По-видимому, наблюдаемая картина связана с фактическим частичным плавлением.


С возрастающей неопределенностью мы можем установить свойства составов с различной долей расплава вблизи солидуса, используя для этой цели линию, полученную Рингвудом [43]. Изменение давления и температуры вдоль этой линии было принято во внимание при применении коэффициентов для оливина. Исправленные значения скоростей приведены в табл. 13.


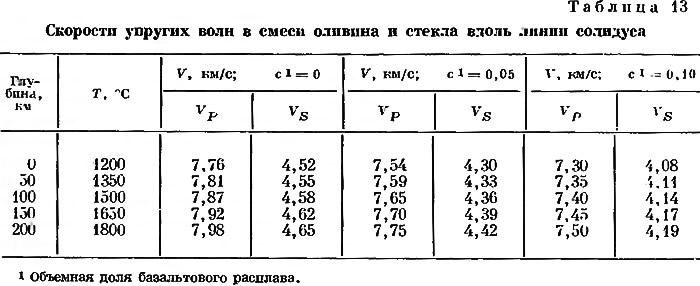
Основные черты модели слоя низких скоростей CIT11A можно объяснить при допущении, что температура солидуса достигается на глубине около 60 км, где она составляет 1400° С. Затем температура возрастает, следуя линии солидуса, при градиенте 3° С/км до глубины примерно 160 км, ниже которой скорость роста температуры становится меньше 3° С/км. Если на глубине 60 и 160 км количество расплава достигает 6°о по объему, минимум скорости будет очень близок к тому, который приводит Андерсон. Средний температурный градиент до глубины 60 км составляет тогда около 23° С/км. однако требуется объяснить возрастание скоростей между 16,5 и 36 км. Если предположить, что в этом слое существует низкий градиент, то необходимо допустить существование более высоких градиентов выше этого слоя, ниже его или в обеих областях. Принимая, что градиент равен 23° С/км, мы получим уменьшение скорости V_Р на 0,2 км/с при увеличении глубины от 16,5 до 36 км. Таким образом, если в этом интервале глубин рост скорости будет происходить согласно модели CIT11A, то либо градиент должен быть ниже, либо влияние температуры должно компенсироваться изменением состава. Возможно, определенную роль играет дегидратация, как это предполагал Рингвуд. Расхождение между вычисленной величиной скорости для оливина, равной 8,06 км/с на глубине 36 км при температуре 840°С, и величиной, полученной из модели CIT11A и составляющей 8,12 км/с, незначительно. Вычисленная скорость для оливина, равная 8,27 км/с на глубине 16,5 км при температуре 390°С, может быть уменьшена до величины ниже 8,06 км,с при замене небольшой части оливина серпентином [12, 13, 23]. Очевидно, если все особенности такого распределения имеют определенное значение, ни одна простая гипотеза не в состоянии объяснить их. При объяснении с позиций частичного плавления исследователи сталкиваются с затруднениями, связанными с основанием слоя пониженных скоростей. Если основание определяется исчезновением расплава и возвращением к исходному (твердому) оливину (или перидотиту), скорости должны вернуться к линии для с=0, возрастая на 0,3 км/с. Однако по модели CIT11A V_Р возрастает на 0,6, а V_S — на 0,16 км/с.

Вывод гутенберговских скоростей на основе «температурного решения» в гомогенном слое обсуждался выше. Минимум V_Р приходится на глубину 80 км, а минимум V_S — на глубину 150 км. Формы распределения, по-видимому, не позволяют привлечь для объяснения частичное плавление, так как интервалы глубин, на которых может существовать расплав, сильно отличаются для двух скоростей.

Было показано, что на глубине 100—120 км различие между скоростями /Овили под океанами и континентальными щитами достигает 0,4 км/с [60]. Если это различие обусловлено только влиянием температуры, то на 100 км (глубины) требуется перепад температур в 1000°С, который кажется невероятно большим. Альтернативное объяснение, т. е. частичным плавлением, требует различия в расплавленной доле на 10% при температурах в обеих областях, близких к солидусу или немного ниже, если под континентами существуют более холодные условия. Приуроченность максимального различия к глубинам между 80 и 110 км грубо соответствует интервалу частичного плавления, который требуется для интерпретации зоны пониженных скоростей по модели CIT11A.

Величины, использованные в этих вычислениях, таковы, что определяемое количество расплава представляет собой верхний предел, так как предполагается, что твердая матрица состоит из оливина. Возможны многочисленные варианты при замене части оливина другими минералами. такими, как гранаты, пироксены и полевые шпаты. Дальнейшим работам в этом направлении должны помочь обсуждения петрологических особенностей, как это сделано, например, в работах Кларка и Рингвуда [24] и Рингвуда [43].

Связь плотности со скоростью

В литературе описано несколько способов определения величины плотности непосредственно из значения сейсмической скорости. Кривая, предложенная Нейфом и Дрейком [40, 41], широко использовалась при сейсмических работах на море. Буллард [64], Тальвани и др. [59] и Штейнхарт и Мейер [58] использовали эмпирические зависимости плотности от скорости для объяснения структуры коры. Для установления более систематических соотношений между изменяющимися плотностью, скоростью, составом, давлением и температурой можно привлечь лабораторные данные по скоростям упругих волн в горных породах в условиях сжатия [11—13, 50, 51, 21, 22, 23, 33].

В настоящей работе мы ограничимся описанием силикатных порол и минералов, представляя их в виде суммы окислов. В этих веществах, несмотря на большое разнообразие в составе и кристаллической структуре, анионы кислорода занимают большую часть объема, а в промежутках между ними расположены меньшие по размерам катионы. Кроме того, в обычных породах средний атомный вес почти всегда заключен в пределах между 20 и 22. Исключение составляют относительно редкие обогащенные железам минералы. Таким образом, плотность указывает на плотность упаковки, которая в свою очередь определяет такие объемные свойства, как сжимаемость и скорости упругих волн.

Рассматривая упругость горных пород, важно предварительно исключить, насколько это возможно, влияние пористости, а уж затем устанавливать присущие породам соотношения. Следовательно, наибольший интерес представляют эксперименты при высоких давлениях. Сопоставление величии Гр, измеренных при давлениях 10 кбар и комнатной температуре [12, 33]. с плотностью показывает, что для обычных пород экспериментальные точки группируются около линии, описываемой уравнением V_Р=a+bp с b≈3 (км/с)/(г/см³). Точки для минералов и горных пород со средним атомным весом больше 22 отклоняются от этой линии более или менее систематически, показывая более низкую скорость для данной плотности или более высокую плотность для данной скорости. Первоначально при попытках освоить эти измерения для каждого вещества с фиксированным средним атомным весом т была подобрана прямая линия. Почти все точки соответствовали m=20—22. Для определения линий, характеризующих более высокие значения m, число точек было недостаточным, и поэтому такие линии были проведены параллельно хорошо установленной линии для m≈21.

Эти линии, во-первых, указывают приближенно на эффект изотермического сжатия для отдельных веществ. Во-вторых, что более важно, они определяют влияние изменения кристаллической структуры, в частности более плотной упаковки, без изменения состава. В-третьих, они указывают на эффект замещения более тяжелыми элементами, такими, как титан или железо. Величины скоростей упругих волн и плотностей, полученные в ходе таких измерений, имеют особенно большое значение при обсуждении вопросов, связанных с верхней мантией и переходной зоной. Так как более прямая информация отсутствует, эти линии могут быть использованы для определения изменения плотности, обусловленного фазовыми изменениями в переходной зоне. В качестве кривых изотермического сжатия точность линий прогрессивно уменьшается с увеличением плотности выше 4 г/см³. Прямые указания на то. каким образом на основании этих измерений установить влияние температуры, отсутствуют, хотя можно представить, что влияние температуры, обратное действию давления, может привести к уменьшению плотности и скорости в отношении, приблизительно представляемом этими линиями. Ниже мы вновь коснемся этого вопроса.

Было предложено несколько способов объединения независимых параметров воздействия плотности и среднего атомного веса в одно соотношение между скоростью и соответствующим параметром. Простейший метод [12] заключается в сопоставлении скорости с отношением ρ/m, которое обратно пропорционально среднему атомному объему. При этом получается почти линейная зависимость, хотя разброс точек больше, чем для зависимости V_P от ρ при постоянной величине m. С таким же успехом можно использовать показатель упаковки vρ/m, предложенный Ферберном, где v — средний объем атомов, рассматриваемых в виде сфер, имеющих радиус иона, определенный. например, Гольдшмидтом (эта величина отличается от среднего атомного объема, который включает «пустое пространство» между сферами).

Андерсон и Нейф [5] построили логарифмическую зависимость модуля объемного сжатия К₀ от среднего атомного объема и нашли соотношение для окислов и силикатов: К₀ = const (ρ₀/m)⁴. Это эквивалентно ф₀ = К₀/ρ₀ = const (ρ³₀/m⁴), или ф₀ пропорционально ρ³₀ при фиксированном значении m.

Аналогичным образом Андерсон [3] связал в одно соотношение m и ф, которое записывается в виде ρ = const (m^aф^b). Константы определяются из экспериментов и в известной мере зависят от выбранных данных. Вероятно, наиболее подходящее решение [3] дает а≈1, b≈1/3. Таким образом, соотношение запишется как ρ = const (mф^1/3), или ρ/m = const ф^1/3. Отсюда ф пропорционально ρ³ для постоянного m.

Скорость ф^1/3, очевидно, почти пропорциональна ρ/m. Если представить, что ф ≈ρ³ является кривой сжатия для данного вещества, то получим К ≈ ρ⁴ и dК/dР = 4.

Более сложный числовой закон был выведен Кноповом [35]. При очень высоких' давлениях' этот закон переходит в решение Томаса — Ферми для элементов и в нем используется «характерный» атомный номер Z вместо естественного среднего атомного числа или среднего атомного веса. Для соединений Z определяется по следующей формуле:


где n_i — процентное содержание элемента с атомным номером Z_i в химической формуле. Кнопов установил, что значения V_Р, ρ для горных пород могут быть представлены либо линейным соотношением


которое для постоянного Z сводится к линейному соотношению между V_P и ρ, либо степенным законом


Величина n получена эмпирически и равна 0,813 ±0,067, или приблизительно 5/6. Опять получаем почти пропорциональную связь между V_Р и ρ. Это обусловлено, конечно, особенностью данных, от которых зависят эти соотношения. Поскольку все данные экспериментальные, они должны совпадать в пределах диапазона эксперимента. Экстраполяция до более высоких плотностей нижней лапши может несколько не совпадать с природной картиной, но необходимость в такой экстраполяции исключается работами по ударному сжатию горных пород. Если плотность может быть найдена независимым путем, например из решений для свободных колебаний Земли, тогда соотношение плотности и скорости накладывает важное ограничение на содержание в веществе мантии тяжелых металлов или железа [15, 3].

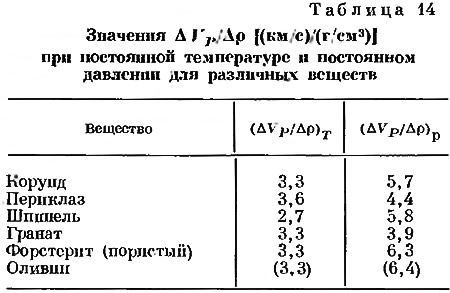
В экспериментах с горными породами или другими агрегатами определяется скорость распространения упругих воли в зависимости от давления при постоянной температуре или в зависимости от температуры при постоянном давлении. Вместе с данными по коэффициентам сжимаемости или тепловому расширению результаты этих экспериментов позволяют определить величину изменения скорости с изменением плотности dV/dp при постоянных давлении или температуре. В среднем отношение dV/dp составляет приблизительно 3 (км/с)/(г/см³) для V_Р, если давление изменяется при постоянной температуре, и несколько больше в случае изменения температуры при постоянном давлении (табл. 14). Однако отношение ΔV/Δρ в качестве отношения конечных разностей, которые могут быть получены для любой пары веществ, может, очевидно, принимать фактически любые значения, так как существуют пары с одинаковой плотностью, но с различными скоростями упругих волн, и наоборот, даже если точки расположены близко к средней линии.


Для слоя однородного вещества при изменении давления и температуры получим


откуда

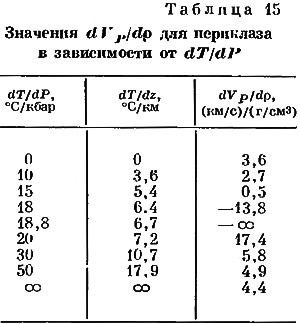
Это выражение характеризуется определенной особенностью при значении (dT/dP) = 1/αKT, представляющем условие для постоянной плотности, если только этот случай не совпадает точно с условием для постоянной скорости. В общем случае это неверно. Рассмотрим в качестве примера изменения dV/dρ в зависимости от величины dT/dP для MgO. Необходимые данные находим в работах Андерсона и его сотрудников: КT=1691 кбар; α=31,4·10^-6°С^-1; ρ=3,58 г/см³; (dVP/dP)_T=7,71·10^-3 (км/с)/кбар; (dVP/dT)_P=—500·10^-6 (км/с)/°С. Используя эти величины (в которых не учитывается влияние давления или температуры), мы получаем результаты, представленные в табл. 15. Чтобы получить dT/dz. нужно dT/dP умножить на 0,358 кбар/км.

Значения dT/dP, равные нулю и бесконечности, как раз и представляют собой коэффициенты для постоянной температуры и постоянного давления соответственно. В применении к верхней мантии мы начнем рассмотрение с высоких температурных градиентов на небольших глубинах, где скорость п плотность уменьшаются по мере увеличения глубины. Предполагая постепенное уменьшение градиента и постоянство состава вещества, мы дойдем до глубины, на которой сжатие компенсирует расширение и градиент плотности обращается в нуль. Однако скорость упругих волн будет еще уменьшаться. dV_P/dρ сначала станет положительной бесконечной величиной, а затем отрицательной бесконечной величиной, когда dT/dP станет меньше 18,8° С/кбар. Между значениями 18,8° С/кбар и 15,6° С/кбар плотность увеличивается с глубиной, тогда как скорость продолжает уменьшаться. Наконец, за этой точкой и плотность и скорость будут увеличиваться с глубиной, и отношение постепенно достигнет предельной величины 3,6 (км/с)/(г/см³). В особом случае, когда (dT/dP)_VP = (dT/dP)_ρ, получим dV/dρ = (K/ρ)(dV/dP)_T независимо от значения dT/dP. Вычисляя это уравнение с помощью приведенных в таблицах величин, получаем результаты, представленные в табл. 14. Таким образом, очевидно, что должны быть найдены отношения такого порядка, за исключением случая близости градиентов к значениям, при которых плотность будет постоянной. При очень высоких давлениях, которые существуют, например, в нижней мантии, отношение ΔV/Δρ, полученное при решении уравнения Адамса — Вильямсона, оказывается близким к 2,4 (км/с)/(г/см³). Небольшая доля уменьшения связана с учетом адиабатического роста температуры, но в основном оно определяется меньшими значениями коэффициентов скорости. Этот пример показывает, насколько опасно принимать однозначное соотношение скорости и плотности для любой области, характеризуемой высоким и изменяющимся температурным градиентом. Ошибка в определении плотности по величинам скоростей не будет большой, но мы не сможем получить однозначного отношения ΔV/Δρ. Большая величина отношения может означать изменение вещества или прохождение через область с критическим температурным градиентом или частичным плавлением. В оливиновой серии замещение магния железом увеличивает плотность, по уменьшает скорость упругих воли, приводя таким образом к отрицательной величине ΔV/Δρ.

Зона пониженных скоростей: изменение содержания железа

По-прежнему предполагая оливиновый состав, представим теперь образование зоны пониженных скоростей при увеличении с глубиной содержания фаялита; при этом в основании зоны должен осуществляться переход к исходному составу, который мы принимаем равным приблизительно Fo₉₀Fa₁₀. Адамс [1] обнаружил, что фаялит, хотя он и плотнее форстерита, более сжимаем. Сжатие, таким образом, увеличивает разность плотностей между этими двумя оливинами, и скорости упругих волн в фаялите оказываются меньше, чем в форстерите. Такой вывод подтверждают измерения скоростей упругих волн в дунитах. Скорости упругих волн в гортополитовом дуните из Бушвелдского комплекса (V_P определялась Берчем [11], а V_S — Симмопсом [50]), имеющем состав, близкий к Fa₅₀, значительно ниже, чем в обычных дунитах, содержащих около 10% фаялита. Опубликованные результаты, однако, ставят ряд проблем, которые мы обсудим ниже.

Образец фаялита, изученный Адамсом, был извлечен из шлака доменной печи и имел плотность (по определению потери веса в бутиловом эфире) 4,068 г/см³. Для чистого синтетического фаялита было получено значение 4,392 г/см³ [65]. Адамс отмечал присутствие в фаялите «некоторого неопределенного вещества, имеющего намного меньший показатель преломления», но полагал, что содержание этого вещества не превышает нескольких процентов и поэтому не исправил данные по сжимаемости. Различие в плотности между образцом и чистым фаялитом требует: 1) чтобы около 7,4% объема составляли пустоты, 2) около 15% объема занимало стекло с плотностью 2,2 г/см³ или 3) присутствовало еще большее количество акцессорного вещества более высокой плотности. В результате может произойти заметное увеличение сжимаемости. Если пустоты смыкаются под действием давления, теория Хасина [31] дает поправку около 17 %, и для твердого фаялита получается значение сжимаемости 0,76 мбар^-1, близкое или немногим меньшее сжимаемости форстерита. Аналогичное уменьшение сжимаемости произойдет при введении поправки на относительно большую сжимаемость значительного количества стекла. Однако, если низкая плотность связана с пустотами, доступными для передающей давление жидкости, измеренная сжимаемость может отвечать действительной. Очевидно, необходимо вновь определить сжимаемость образца фаялита, имеющего истинную плотность.

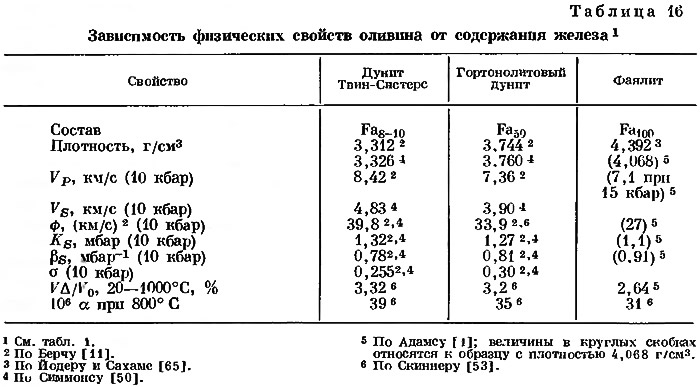
По-видимому, лучше всего использовать прямые определения скоростей упругих волн в гортонолитовом дуните. В табл. 16 представлены эти скорости, а также другие выведенные величины. Гортонолитовый дунит — грубозернистая порода, содержащая свыше 90% гортонолита состава ~Fa₅₀ и небольшие переменные количества диаллага, роговой обманки и окислов. Химический анализ бушвелдских образцов был опубликован Вагнером в 1929 г.; впоследствии анализ был повторен Берчем [12]. Плотность этого образца составляет около 3,83 г/см³. Шесть образцов, изученных Берчем и Симмонсом, имели плотность от 3,707 до 3,828 г/см³. Они были слабо изменены, что привело, вероятно, к некоторому снижению плотностей и скоростей упругих волн по сравнению с неизмененным гортонолитом. Оливин состава Fo50Fa50 имеет теоретическую плотность 3,80 г/см³.


Коэффициенты теплового расширения гортонолита и форстерита заметно пе отличаются [52, 53]. Таким образом, в соответствии с вышеприведенным обсуждением мы принимаем, что относительное изменение скоростей упругих волн при изменении температуры в гортонолите такое же, как и в форстерите, и в таблицу зависимостей скоростей от глубины для гортонолита вносим значения, полученные путем умножения соответствующих величин для форстерита (табл. 11) на отношение скоростей при комнатной температуре и давлении 10 кбар. Результаты такого подсчета приведены в табл. 17 и на фиг. 6. На фиг. 6 представлено также распределение скоростей сейсмических волн, полученное по модели CIT11A, и ряд интерполированных значении для Fa₃₀. Распределение скорости V_Р может определяться увеличением содержания фаялита от 10% до 24% при наименьшем значении скорости и возвращением к исходному содержанию 10% в основании зоны пониженных скоростей. Для скорости V_S интерполированный состав, отвечающий минимуму скоростей, соответствует 21% фаялита. Таким образом, не прибегая к существенному пересмотру картины распределения скоростей или температур, минимум в распределении скоростей можно объяснить наличием обогащенного железом слоя (до 23 ±2% фаялита) на глубинах приблизительно между 90 и 140 км.


В соответствии с этой интерполяцией зона пониженных скоростей характеризуется более высокой плотностью по сравнению с вышележащими и нижележащими слоями. По-прежнему принимая оливиновый состав, а также пренебрегая малыми и почти скомпенсированными поправками на давление и температуру, мы получаем, что плотность в зоне с минимальной скоростью равна около 3,48 г/см3 (Fa₂₃).

Хотя использованные в наших вычислениях величины верны строго (в пределах различного рода ошибок) только для оливиновой серии, полученные выводы могут быть качественно справедливыми и для вероятно присутствующих в верхней мантии более сложных перидотитов, содержащих гранат, пироксен или другие минералы, так как они как будто характеризуются такой же зависимостью плотности и скорости упругих волн от содержания железа, как и оливины [12, 13]. Как и при рассмотрении частичного плавления, объяснение, основанное на обогащении железом, дает совпадение зон пониженных скоростей волн Р и S по глубине.