Однако, даже в том случае, если оси кристаллов ориентированы случайно, неравномерное распределение горизонтальных напряжений может вызвать анизотропию скоростей. Немногочисленные наблюдения подтверждают этот эффект. Так, Точер [9], проводивший измерения на гранитах, установил различие в скоростях, равное примерно 9%, при разности напряжений ~1 кбар. Он пришел к выводу, что данные измерения анизотропии скоростей волн могут служить показателем накопления энергии деформаций в сейсмически активных зонах, как. например, в зоне разлома Сан-Андреас.
Однако на практике при проведении полевых работ методом преломленных волн исследователи, как правило, игнорировали в своих анализах строения коры возможность анизотропии. В подробной сводке результатов, полученных по преломленных! волнам, Штейнхарт и Мейер [8] не упоминают о явлении анизотропии. Специальных работ, посвященных установлению этого эффекта, почти не проводилось. Горизонтальные изменения скорости, если они наблюдались, объясняли региональными изменениями состава или физического состояния пород.
Правда, Хесс [4] обратил внимание на то, что измерения Шора и Райтта в северо-восточной части Тихого океана к югу от 45° с. ш. свидетельствуют о связи между скоростью волн и направлением профиля. Казалось, что почти все изменения можно объяснить анизотропией скоростей с максимумом 8,6 км/с (направление на восток) и минимумом 8,0 км/с (направление на север). Однако эти данные получены в результате редких измерении, рассеянных в обширной области между Калифорнией и Гавайскими островами. Поэтому можно считать, что изменения скоростей обусловлены различием среды в пунктах наблюдения. Другими словами, хотя анизотропия и согласуется с наблюдениями, она ими не доказана. Для доказательства ее существования необходимо, чтобы наблюдения от одного источника волн велись в разных направлениях в одной и той же среде.
Изучение анизотропии
Баккус [1 I показал, что функция, описывающая в самом общем виде зависимость горизонтальной компоненты скорости продольных волн v от азимута ф, имеет следующий вид:
причем ф измеряется от востока против часовой стрелки.
В принципе пять постоянных уравнения (1) можно определить, выполнив пять измерений скорости в пяти различных азимутах. На практике, однако, существует значительная погрешность наблюдений, и, чтобы удовлетворительно описать анизотропию, требуется выполнить гораздо больше пяти измерений. Кроме того, эти измерения должны быть распределены по возможности равномерно по азимутам.
Океанографический институт Скриппса провел изучение анизотропии по программам «Квартет» и «Флора». Исследованные участки показаны на фиг. 1; они были выбраны в основном потому, что это ближайшие к Сан-Диего районы, сравнительно свободные от подводных гор, где к тому же ранее уже проводилось сейсмическое зондирование преломленными волнами. Кроме того, разносторонние исследования проводились в районе Гавайских островов; их результаты изучаются.
Расположение пунктов взрыва и приемников приведено на фиг. 2 и 3. Пунктов регистрации было слишком много, чтобы все их можно было нанести на схему; поэтому указаны лишь направления для отдельных профилей. Изображены только те пункты взрыва, для которых зарегистрированы вступления от мантии. Не отражены многие взрывы, регистрировавшиеся на коротких профилях для выделения вступлений от более мелких горизонтов.
Подробные данные о временах пробега и расположении всех этих пунктов приведены в работе Райтта и др. [5].
Анализ полученных данных
Обычные методы интерпретации неприменимы для работы такого типа, как данная. Эти методы, опирающиеся на допущение о постоянной скорости волн в слоях с неизменным углом падения, можно использовать для анализа простых структур и расположения пунктов взрыва и приемников на коротких профилях. В нашем же случае скорость анизотропна, а пункты взрыва и приемники распределены на большой площади.
Гарднер [3] предложил метод интерпретации преломленных волн для наблюдений, распределенных по площади, который легко приспособить к изучению анизотропии, когда приемники неизбежно должны быть распределены на большой площади. Сходные методы описали Уилмор и Банкрофт [12], а также Шейдеггер и Уиллмор [6]. Эта методика была широко использована Берри и Уэстом [2] и Смитом и др. [7] при обработке данных экспериментального взрыва на озере Верхнем в 1963 г.
По методике Гарднера — Уиллмора определяют приближенное соотношение для Т — времени пробега волны, преломленной в мантии, между пунктами А и В поверхности Земли, находящимися на расстоянии d:
где v — скорость волн в мантии. τA и τB были названы Гарднером временами запаздывания, поскольку они соответствуют времени, которое волны затрачивают в пунктах А и В для пересечения коры. Если для пунктов А и В известен разрез скоростей коры, то по времени запаздывания можно определить глубину подошвы коры.
Анализ данных, распределенных на площади, заключается по этой методике в регистрации времен пробега во многих пунктах приема от расположенных относительно них должным образом многих пунктов взрыва. Каждое измеренное время пробега позволяет составить уравнение типа (2). Регистрируя каждый взрыв в нескольких пунктах приема, мы получаем гораздо больше уравнений, чем неизвестных параметров τ. Решая систему методом наименьших квадратов, получаем наилучшие значения τ и скорости v. Если скорость v зависит от угла ф, то уравнение (2) становится нелинейным в связи с изменениями скорости в знаменателе первого члена его правой части. Однако, поскольку анизотропия мала, уравнение (2) с помощью простого преобразования можно свести к линейному, так что при решении системы уравнений окажется возможным использовать способ наименьших квадратов:
где A'=A/v20, B'=B/v20 и т. д., a A — среднее расстояние по горизонтали между положением пункта взрыва или приема и местом, где преломленная волна вступает в мантию или покидает ее.
На суше нетрудно использовать любой пункт взрыва или приема столько раз, сколько нужно, однако при проведении глубинного сейсмического зондирования на море это фактически невозможно в связи с навигационными трудностями и дрейфом судов, ведущих прием. Таким образом, на море местоположения пунктов взрыва или приема не могут совпадать и, строго говоря, число неизвестных всегда должно превышать число уравнений.
При исследованиях «Квартет» и «Флора» это затруднение удалось устранить, допустив, что времена запаздывания могут быть описаны функцией местоположения соответствующих пунктов, которая полностью определяется ограниченным числом параметров. Утверждение, что можно ограничиться таким числом параметров, которое мало по сравнению с числом пунктов регистрации и взрыва, равносильно допущению, что уклоны преломляющих границ и градиенты уклонов малы, а это допущение присуще и самому методу с использованием времен запаздывания.
Принятая нами методика решения имеет и то преимущество, что позволяет уменьшить порядок матрицы при решении уравнений по способу наименьших квадратов. При обычной методике порядок матрицы определяется числом пунктов взрыва и приема. Берри и Уэст [2] при решении своей задачи были вынуждены ограничить суммарное число пунктов взрыва 117, так как использовать большее число пунктов не позволяла программа перевода уравнений на матричную форму решения. При анализе испытаний «Квартет» и «Флора» удалось получить удовлетворительное решение, пользуясь всего 24 параметрами, хотя при испытании «Квартет» было зарегистрировано 289 взрывов, а при испытании «Флора» — 303.
Функция, используемая для описания «поверхности» времен запаздывания, может иметь самую разнообразную форму. Предполагается, что эта функция может быть найдена при решении системы уравнений способом наименьших квадратов. Для описания данных, полученных при исследованиях «Квартет» и «Флора», мы использовали функцию с 19 параметрами; соответствующая поверхность представляла плоский склон, на который был наложен двойной ряд Фурье, содержащий 16 членов. Таким образом, получалось 3 члена на описание склона, 16 членов ряда Фурье и еще 5 членов, отражающих функцию скорости согласно уравнению (1), а всего 24 параметра.
Упомянутое уравнение поверхности имеет следующий вид:
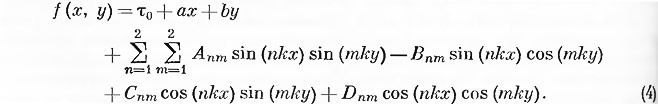
Поверхности, отражающие решение этих уравнений, показаны на фиг. 4 и 5 с контурами изолиний запаздывания времен пробега в районах осуществления программ «Квартет» и «Флора». Как видно на фиг. 2 и 3, пункть взрыва и приема при этих исследованиях распределены весьма неравномерно Поэтому неясно, насколько значимы изолинии фиг. 4 и 5 на участках, где отсутствовали пункты взрыва или приема. Плавный характер функций описывающих решение, отражает существенное сглаживание данных о временах запаздывания; так же плавно проводилась интерполяция для участков, где наблюдений не велось. Такая интерполяция может оказаться спорной; в качестве прогноза для еще не изученной территории она, вероятно, совсем непригодна.
Анизотропия
Форма «поверхности» запаздывания времен заслуживает специального изучения, но в работе, посвященной анизотропии и нацеленной прежде всего на определение вариаций скорости, «рельеф» такой поверхности только мешает определению скоростей, и его влияние при измерениях скорости должно быть исключено. Окончательные данные о пяти коэффициентах, характеризующих анизотропию скоростей для обоих районов испытаний, приведены в табл. 1.
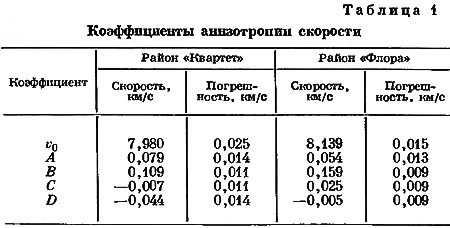
Как видно из таблицы, величина коэффициентов А ш В при членах sin 2ф и cos 2ф (из соотношения Баккуса для анизотропии) намного выше значения средней квадратичной ошибки. Более того, значения этих коэффициентов в районах исследований по программам «Квартет» и «Флора» примерно согласуются. С другой стороны, величина коэффициентов С и D соизмерима с соответствующей им погрешностью, и они различны для этих районов. Величины D для района «Квартет» и С для района «Флора» статистически значимы, если погрешности распределены случайно. Однако возможность систематической ошибки заставляет считать члены с углом 4ф менее надежными, чем с углом 2ф.
Если считать статистически значимыми только члены с углами 2ф. то описание анизотропии упростится, поскольку в соотношении Баккуса останутся лишь коэффициенты А и В. При определении анизотропии только через А и В она оказывается почти одинаковой в обоих исследованных районах. Так, угол ф направления максимальной скорости в районе «Квартет» равен 18°, а в районе «Флора» 9°. Соответствующие значения обычных азимутов равны 72 и 81°, что согласуется с азимутом направления максимальной скорости, вычисленным Баккусом [1] с учетом данных всех измерений скорости в Тихом океане к западу от побережья штатов Калифорния и Орегон. Правда, величина анизотропии в районах «Квартет» и «Флора» значительно меньше. Разность между максимальной и минимальной скоростью (рассчитанная только с учетом коэффициентов А и В) составляет по данным испытаний «Квартет» 0,27 км/с, «Флора» 0,34 км/с, а по совокупности наблюдений, учтенных Баккусом, 0,54 км/с.
Все это представляется приемлемым, так как если даже считать, что анизотропия одинакова по всей части Тихого океана к западу от побережья Калифорнии и Орегона, то ее кажущееся по наблюдениям значение может быть искажено за счет географического фактора, обусловливающего систематическую зависимость азимута скорости от местоположения. Следовательно, хотя данные испытаний «Квартет» и «Флора» свидетельствуют в пользу существования анизотропии в соответствующих районах, они не обязательно доказывают, что анизотропия выражена во всем упомянутом районе Тихого океана. Сейчас получается, что величина анизотропии по данным совокупности наблюдений примерно вдвое больше, чем для районов «Квартета и «Флора». Представляется вполне оправданным вывод, что примерно половина этой наблюдаемой анизотропии приходится на географический фактор, а половину можно приписать собственно анизотропии.