Одно из главных затруднений, возникающих при создании сейсмической модели верхней мантии, связано с технологией изготовления среды, где скорость волн непрерывно изменяется. Поэтому на первых норах создавались двумерные модели. Было разработано несколько типов таких моделей [5]: биморфные (ряд листов различного материала и различной толщины, соединенных путем склеивания, оплавления, электролиза и т. д.): перфорированные (дырчатые листы с различным диаметром отверстий и изменяющейся густотой их распределения); термические (пластины, изготовленные из специального материала, в котором под влиянием температуры скорость волн изменяется заданным образом). Недавно удалось создать трехмерные модели с непрерывным изменением скорости волн, которые состоят из большого числа тонких слоев; при этом разность в скорости волн у соседних слоев пренебрежимо мала. В качестве моделирующей среды использовались многокомпонентные гели [15, 16] или клейкие смолы, цементирующие кварцевый песок [12].
Следует подчеркнуть, что пока возможности сейсмического моделирования и соответствующей теории ограничены. Чрезвычайно трудно (почти невозможно) найти моделирующую среду, которая воспроизводила бы все свойства прототипа. Если, например, скорости моделируются в надлежащем масштабе, то параметры затухания могут не удовлетворять законам подобия при моделировании. Поэтому обычно сейсмические модели позволяют получить лишь качественное решение для частных задач.
В настоящее время основное значение сейсмического моделирования состоит в том, что оно позволяет изучать динамические параметры сейсмических волн для таких случаев, где теория не дает полноценного решения. Для верхней мантии особое значение имеют два вопроса — о слое-волноводе и о зонах, где при непрерывном изменении скорости терпит разрыв ее градиент. Оба вопроса изучались методом сейсмического моделирования.
Волноводы. Поскольку слой с пониженной скоростью волн может служить волноводом, с помощью сейсмических моделей было изучено несколько типов волноводов с резкими и нерезкими границами. При этом рассматривалось распространение объемных волн Р и каналовых волн типа Ра, а использовались в основном двумерные модели.
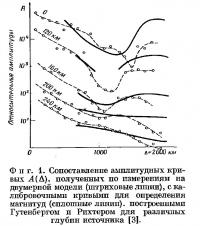
Ризниченко и Шамина посвятили несколько статей анализу амплитудных кривых волн Р па двумерных биморфных моделях с различным вертикальным распределением скоростей волн. Они нашли, что в среде с отрицательным градиентом скорости уменьшение амплитуд, зависящее от эпицентрального расстояния, проявляется сильнее, чем для случая постоянной скорости волн или положительного градиента скорости [9]. У моделей с волноводом отмечался четкий минимум на соответствующих амплитудных кривых, когда источник волн помещался над волноводом или в его пределах. Положение минимума на кривой соответствовало эпицентральным расстояниям. на которых отмечается зона тени, и смещалось в сторону меньших расстояний по мере возрастания глубины источника [10]. Данные проведенных экспериментов с моделями в целом согласуются с калибровочными кривыми для магнитуд (фиг. 1), полученными Гутенбергом и Рихтером [3].
Довольно многочисленные эксперименты на моделях проводились в связи с изучением характера волн Ра и Sa, которые интерпретировались как каналовые волны, распространяющиеся в волноводе верхней мантии. Пользуясь двумерной моделью, состоящей из парафиново-полиэтиленового слоя между двумя листами плексигласа, Хорошева [2] показала возможность регистрации каналовых волн типа Ра и Sа на поверхности Земли. Капцан и Кисловская [6] провели эксперименты с несколькими двумерными перфорированными моделями; они стремились выяснить механизм возбуждения каналовых волн. На явно колебательный характер амплитудных кривых волн Ра указывают как данные, полученные на моделях, так и наблюдения над амплитудами глубокофокусиых землетрясений с магнитудами выше 6,5. В целом экспериментальные данные показывают, что гипотеза Калои о природе волн Ра и Sa более вероятна, чем гипотеза «шепчущей галереи», выдвинутая Прессом и Юингом.
Несомненно, результаты, полученные при двумерном моделировании, весьма интересны. Однако в принципе неясно, окажется ли моделирование пространственного процесса распространения волн на пластине достаточным приближением к действительности, особенно если учитывать динамические параметры волн [7].
Поэтому Шамина [12] поставила вопрос о показателях, необходимых н достаточных для выделения волновода, и изучала его на трехмерных моделях из клейких смол с различным содержанием кварцевого песка. Подтвердив некоторые результаты, полученные на двумерных моделях, она уделила особое внимание кривым изменения амплитуды с глубиной A(h) для волн Р в зоне тени. Данные наблюдений показали, что минимум этих кривых приходится на глубину, примерно соответствующую минимуму7 скорости на разрезах скоростей. Сходный характер имеют кривые изменения амплитуд с глубиной, полученные для глубокофокусных землетрясений в районе хребта Гиндукуш (фиг. 2). Проведенное сопоставление указывает на возможность существования в Центральной Азии слоя-волновода с минимумом скорости волн Р па глубинах 140—180 км.
Разрывы градиента. Опубликовано очень мало работ по моделированию, которые затрагивали бы важный вопрос о среде с разрывами в градиенте скоростей войн. Недавно проведенные эксперименты с трехмерными моделями земной коры, представляющими слои, где скорости волн непрерывно изменяются [4, 17], показали, что при интерпретации данных глубинного сейсмического зондирования необходимо учитывать и амплитуды сейсмических волн.
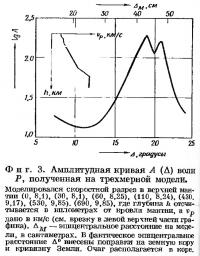
Чтобы объяснить поведение амплитудных кривых волн Р, полученных по данным о неглубоких землетрясениях, мы провели эксперименты с рядом трехмерных моделей верхней мантии [14]. Они учитывали существование слоя-волновода и разрывов второго порядка (градиента скорости); в качестве моделирующей среды использовались многокомпонентные гели. Чтобы проиллюстрировать проведенную работу, приводим на фиг. 3 амплитудную кривую волн Р, соответствующую средним данным по трем моделям с идентичным разрезом скоростей. На врезке в левой верхней части фигуры схематически показан и сам разрез скоростей, для которого характерен слабо выраженный волновод и разрыв второго порядка. Параметры подобия (масштаба), характеризующие модель: svP = 0,185, sT = 1·10-6, sλ = 1,85·10-7, где индексы v, Т и λ относятся соответственно к скорости волн Р, их периоду и длине. Опираясь на эту модель, мы предложили возможную схему строения верхней мантии в юго-восточной Европе (см. стр. 202).
Хотя методы сейсмического моделирования не позволяют дать окончательную количественную интерпретацию сейсмических наблюдений, дальнейшие исследования в этом направлении представляются насущно необходимыми. Этот взгляд был подчеркнут и на первом Симпозиуме по сейсмическому моделированию, состоявшемся в 1965 г., где подводились итоги развития этого направления и отмечалось его место в общем комплексе сейсмологических исследований.