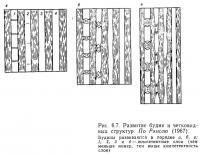
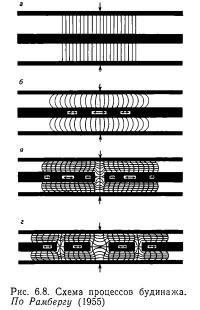
В общем, будины образуются, когда горные породы, которые текут относительно затрудненно, образуют блоки в породах, которые текут более легко. В разрезе эти блоки имеют продолговатые фигуры, которые находятся относительно близко от мест первоначального залегания. Концы продолговатых тел могут удлиняться, придавая им линзообразную форму, обусловленную пластической деформацией, или они могут образовывать так называемые четковидные структуры (pinch and swell structures), как бы присоединяясь к соседним линзам. Полагают, что формирование этих типов обусловлено общей причиной. Некоторые примеры будин показаны на рис. 6.7 и 6.8.
Будины изучались многими геологами, начиная с 1909 г., когда Лохест впервые описал их в бельгийском песчанике, дав им это название. Позднее были выполнены экспериментальные и теоретические исследования, а также приведены описания и классификация будин. Математический анализ механизма будинажа был предпринят, в частности, Рамбергом (1955) и Гзовским [47]. Равно как и складки, будины представляют собой очень важные структуры для определения механических условий, преобладавших во время их образования. В этом разделе мы остановимся на самых основных типах будинажа.
Когда система, состоящая из чередующихся некомпетентных и компетентных слоев, подвергается сжатию под прямым углом к напластованию, компетентные слои растягиваются под действием течения некомпетентных слоев. Если компетентные слои способны в некоторой степени испытывать пластическую деформацию, они будут образовывать четко- или линзообразные структуры в зависимости от степени их компетентности. Если появляются хрупкие трещины растяжения, то будут возникать типичные будины (рис. 6.8). Рамберг (1955) полагал, что течение некомпетентных слоев будет характеризоваться вязким течением, а поведение компетентных слоев вплоть до возникновения трещин будет соответствовать упругой деформации. Он предложил следующие теоретические условия образования будин:
где zb и zd — мощности компетентного и некомпетентного слоев; Р0 и Р1 — давления в центре и у концов компетентного слоя, длина которого 2l; St — прочность на разрыв компетентного слоя.
Итак, когда Р0—Р1 заключается в пределах, задаваемых этим неравенством, будет возникать будина длиной 2l. Р0—P1 рассчитывается по следующему уравнению:
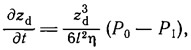
где η — вязкость некомпетентного слоя; δzd/δt — скорость сокращения толщины слоя.
Рамберг рассчитал; что δzd/δt = 10-11 см/с, принимая, что Р0—P1 = 5 МПа, zd = 100 см, l = 75 см и η = 1019 Па·с. Так как эта скорость эквивалентна примерно 3 см за 10 тыс. лет, он считал, что эта величина показывает приемлемую скорость, с которой слои могли бы сжиматься в реальности, но его оценка Р0—P1 не подтверждена конкретными доказательствами. Рассмотрим пример более широкого применения анализа Рамберга к реальным будинам, изученным в поле (Уемура, 1965, 1971).
Южная часть комплекса Шиманто, развитого на п-ове Кии, называется серией Муро, сложенной группой палеогеновых — нижнемиоценовых отложений. В группе Муро преобладают чередующиеся песчаники и глинистые сланцы. Песчаник иногда образует будины. Следовательно, слои песчаника и глинистого сланца играют роль компетентных и некомпетентных слоев, соответственно. Геологические съемки проводились на обширной территории, и были измерены размеры группы будин. Средние значения длины будин (2l) составляли 28 см, толщины (tb) = 12 см, мощности промежутков глинистого сланца между буди-нами (td)—15 см. Принимая среднее значение δzd/δt и исключив Р0—Р1, которое нельзя измерить, из двух уравнений Рамберга, получаем
Поскольку полевые наблюдения показали, что степень деформации не была очень большой, если принять, что zb = tb и 2d = td, то величина δzd/δt, связанная со скоростью течения глинистого сланца, которое образует будины, определяется двумя физическими константами St и η.
St — это сопротивление разрыву песчаника в то время, когда, образовались будины, поэтому значения, измеренные на современных образцах, нельзя использовать в том виде, в каком они получены. Обработка данных по значениям, замеренным для японского песчаника всех геологических возрастов, позволила построить график, показывающий примерную зависимость его прочности от возраста. По этому графику для времени образования будин (вероятно, совпадающему с возрастом складчатости) в группе Муро были получены значения 1—4 МПа. Сопоставимые значения (3—5 МПа) были получены по результатам испытаний на радиальное сжатие образцов неправильной формы песчаника Муро. Оставшийся конечный элемент — коэффициент вязкости η. Принимая, что η = 1021 Па·с, а это подтверждается различными исследованиями течения материалов земной коры, δzd/δt как скорость деформации дает значение около 1—0,3·10-14. Если бы глинистый сланец тек со скоростью, которая уменьшала бы его толщину на 3—1 см за 1 млн. лет, то образовались бы будины, напоминающие наблюдаемые в действительности.
С другой стороны, поскольку складчатая группа Муро с угловым несогласием перекрывается отложениями среднего миоцена, период складкообразования ограничен несколькими миллионами лет между ранним и средним миоценом. Полученная выше скорость деформации не противоречит этому факту. Однако, можно предполагать, что значение 1021 Па·с показывает верхний предел вязкости осадочных пород, поэтому, если η = 1020 Па·с, была бы получена в десять раз большая скорость деформации, и тогда образование складок группы Муро завершилось бы за несколько десятков тысяч лет. Напротив, если бы мы действительно смогли определить продолжительность периода складкообразования, то могли бы рассчитать вязкость. В основном, однако, мы не можем прибегнуть к этому методу. Любое количественное обсуждение этой проблемы зависит от возможности получения точного значения для коэффициента вязкости. Если эта задача была бы решена, тогда можно было бы установить механические условия, преобладавшие во время будинажа, такие, например, как величина сил, обусловивших течение глинистого сланца, и градиент давления в направлении течения. Любой механический анализ геологических структур, образованных течением горных пород и формаций, в конце концов сводится к выяснению взаимосвязей между скоростью деформации, коэффициентами вязкости и напряжением. Проблемы, связанные с механизмами развития структур будинажа, не составляют исключения.