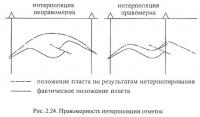
Поскольку реальные сети наблюдений обладают определенной степенью избыточности в части выявления основных структурных элементов гипсометрии, решение вопроса о правомерности интерполяции отметок в межскважинном пространстве можно осуществлять на основе известного метода разрежения разведочной сети.
Для производства оценки необходимо выполнить построение функции (условно названной кривой разведанности), связывающей значения ламбда-критериев разведанности и площади проекций оценочных четырехугольников (Sбл), т. е. функции λ=f(Sбл).
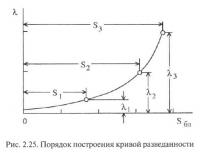
Построение кривой предусматривается производить путем разрежения разведочной сети (рис. 2.25). Для этого по исходной квадриангулированной сети наблюдений рассчитываются среднеарифметические значения ламбда-критериев (λ1) и площадей проекций выделенных оценочных блоков (S1).
Затем производится примерно двукратное разрежение исходной сети, вновь рассчитываются критерии разведанности, площади и определяются их средние значения (λ2 и S2). И наконец, сеть подвергается еще одному разрежению, с последующим вычислением по его результатам средних значений λ3 и S3. Полученные точки наносятся на график и соединяются плавной линией — кривой разведанности. Естественно, что эта кривая теоретически должна иметь характер монотонно возрастающей функции (рис. 2.25), т. к. по мере снижения плотности сети точек наблюдений достоверность результатов горно-геометрического моделирования должна постоянно уменьшаться.
Использование именно данной методики построения кривой разведанности связано со следующим обстоятельством. Поскольку значение ламбда-критерия определяется не только плотностью сети наблюдений, но и сложностью геологического строения изучаемого объекта, то при построении функции λ = f(Sбл) необходимо нейтрализовать действие фактора сложности. Достичь этого можно только путем его фиксации, т. е. путем обеспечения постоянства сложности для всех точек графика. Так как равномерное разрежение сети наблюдений и последующее осреднение получаемых значений охватывают весь объект геометризации, то, по-видимому, средняя сложность объекта для каждой из точек графика должна автоматически быть постоянной.
Построение кривой разведанности без разрежений (т. е. путем простого построения зависимости значений ламбда-критериев от площадей четырехугольников, выделенных по исходной сети замеров) методически неверно и приводит, вне зависимости от степени соответствия густоты точек измерений и сложности геологического объекта, к возникновению не только размытой, но и противоестественной картины. Это связано с тем, что сложность строения изучаемого объекта практически всегда переменна. Зоны повышенной сложности имеют более низкую степень разведанности, чем простые, несмотря на то, что плотность разведочной сети по ним, как правило, выше. Более того, при идеально выполненных разведочных работах в пределах контуров одинакового назначения (например, контура первоочередного освоения) рассматриваемая функция должна иметь вид: λ = f(Sбл) = const, отражая тем самым идеально постоянный уровень достоверности запасов. Всякое частное отклонение от этого уровня должно квалифицироваться либо как переразведка, либо как недоизученность.
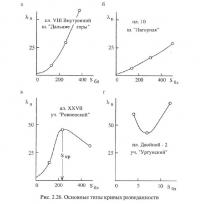
Экспериментально установлено, что встречаются три основных типа кривых разведанности (рис. 2.26).
К первому типу (рис. 2.26, а и б) относятся кривые, имеющие вид, соответствующий теоретически ожидаемому. Такие кривые характерны для хорошо изученных объектов, плотность разведочной сети по которым обеспечивает правомерность интерполяции отметок в меж-скважинном пространстве.
Дополнительно по степени крутизны ветви графика функции λ = f(Sбл) можно судить о возможном росте общей степени разведанности объекта при дальнейшем повсеместном сгущении разведочной сети. Отметим также, что величина свободного члена функции (ожидаемое значение λ при Sбл = 0) теоретически должна быть равна удвоенной среднеквадратической погрешности определения координат Z пластоподсечений и является таким образом дополнительным параметром, контролирующим надежность построений.
Второй тип кривых разведанности (рис. 2.26, г) имеет вид, совершенно противоречащий теоретическому. Анализируя такие кривые, можно было бы сделать абсолютно абсурдный вывод о возможности снижения точности геометрической модели пласта при увеличении плотности разведочной сети. Понятно, что такое поведение кривой возможно лишь в случае, когда малейшее разрежение исходной сети повсеместно и постоянно приводит к полной потере информации об отдельных структурных элементах пласта. Причем нет никакой гарантии и того, что эта исходная сеть замеров действительно вскрыла все крупные структурные элементы. Поэтому такие кривые характерны для объектов, плотность разведочной сети по которым не обеспечивает правомерности интерполяции отметок в межскважинном пространстве.
Третий, промежуточный, тип кривой (рис. 2.26, в) объединяет в себе оба предшествующих типа. Вначале, по мере роста площадей оценочных блоков, происходит рост неоднозначности построений (теоретически ожидаемая тенденция — кривая первого типа), а затем — ее снижение (кривая второго типа). Данный тип характерен для слаборазведанных объектов и вполне естественен. Исходная сеть наблюдений позволяет с гой или иной погрешностью выявить основные структурные элементы пласта, но при ее значительном разрежении наступает такой момент, когда информация о них начинает теряться. Естественно, что к такому типу можно привести путем производства четвертого и последующих разрежений исходной сети замеров и кривые, приведенные на рис. 2.26, а и в. Поэтому для кривых данного типа следует сделать вывод об ограниченной правомерности интерполирования высотных отметок в межскважинном пространстве: для оценочных блоков с площадью меньшей критической (Sкр — рис. 2.26,в) она существует, а для большей — отсутствует.
При получении кривой рассматриваемого типа среди реально выделенных оценочных блоков выделяются блоки с площадями менее Sкр, для которых правомерно осуществлять расчет ламбда-критериев. По остальным (закритическим) блокам сети такой расчет выполнять нецелесообразно в связи с его низкой надежностью. Такие закритические по площади блоки могут размещаться по площади участка либо концентрированно, либо хаотически. В первом случае участок как бы разделяется на две части, анализ материалов по одной из которых (с малыми площадями блоков) может производиться с помощью ламбда-критериев, а для другой они в принципе неприменимы. Во втором случае может возникнуть опасная ситуация, когда при значительном количестве за критических блоков (более 30 % от общего количества четырехугольников сети замеров) реально имеющая место погрешность в оценке значения Sкр может привести к ошибочному представлению о якобы возможном интерполировании отметок пласта между точками измерений. Поэтому при значительной доле закритических блоков целесообразно вообще отказаться от расчета ламбда-критериев.
Выполнение разрежения исходной разведочной сети может выполняться либо интерактивно (путем непосредственного выделения оператором разреженных блоков на экране ЭВМ в программе «DRU»), либо автоматически (программой «PRNGEO»). Алгоритм автоматического разрежения сети состоит в следующем (рис. 2.27).
На рассматриваемый участок параллельно геодезическим осям координат Хи ^накладывается квадратная сетка со сторонами, равными среднему расстоянию между замерами G. Причем крайние верхняя и правая линии сетки должны совпадать с точками измерений, имеющими максимальные значения соответствующих координат. В этом случае каждый замер попадет в отдельный квадрат сетки. Столбцы и строки сетки нумеруются целыми числами (начиная с нуля) в направлении уменьшения значений координат. При первом разрежении сети (перед автоматическим ее квадриангулированием) исключаются измерения, попавшие в расположенные в шахматном порядке квадраты сетки (имеющие нечетные номера по оси Y при четных номерах по оси X и четные номера по оси Y при нечетных по оси X). А при втором разрежении дополнительно исключаются все замеры, попавшие в четные по оси Y квадраты. Естественно, что описанный алгоритм реализует только один из возможных вариантов разрежения сети наблюдений.
Практически при построении кривых разведанности выполняется несколько вариантов однократного и двукратного разрежений как на экране ЭВМ (в программе «DRU»), так и автоматически (в программе «PRNGEO» — путем принятия противоположного вышеописанному порядка выделения исключаемых квадратов сетки). Кривые, построенные по различным вариантам разрежения, должны давать одинаковые оценки правомерности интерполяции. Однако если получаемые результаты неоднозначны (хотя на практике, при построении почти ста кривых разведанности по различным пластам, такого явления ни разу не наблюдалось), то в качестве итогового решения должно приниматься наиболее неблагоприятное.
Таким образом, в результате проведения оценки правомерности интерполирования могут быть получены три различных вывода:
- интерполяция правомерна;
- интерполяция правомерна в оценочных блоках с площадью менее Sкр;
- интерполяция неправомерна.
Таблица решений, позволяющая производить их выбор, приведена и табл. 2.9. При пользовании таблицей следует обратить внимание на три следующих обстоятельства.
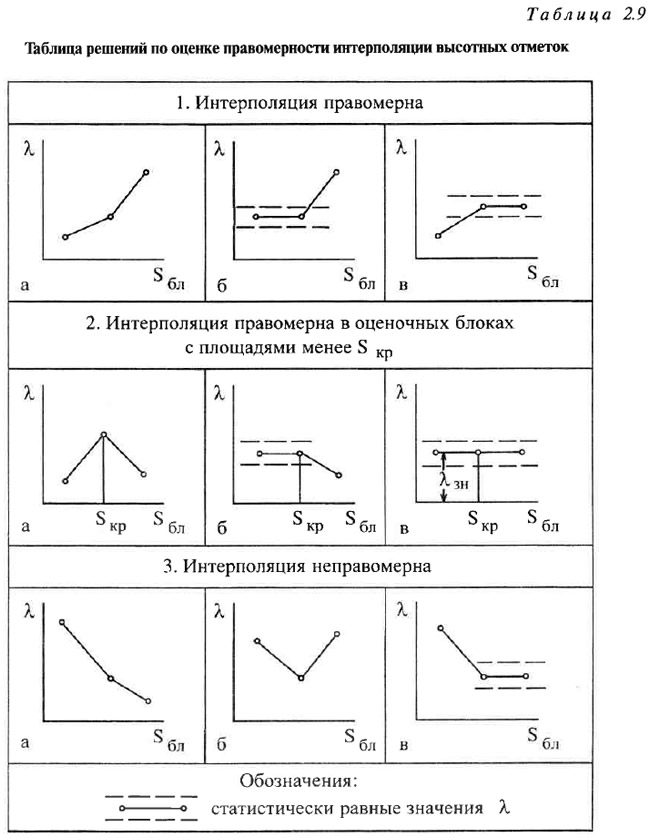
Во-первых, при получении второго решения не следует забывать о ранее указанной допустимой доле закритических оценочных блоков.
Во-вторых, в случае, если последующая точка графика имеет среднее значение ламбда-критерия меньше чем предыдущая, проверяется гипотеза о статистическом равенстве этих значений.
Гипотеза проверяется по известной методике [9]. Для этого определяются параметры:
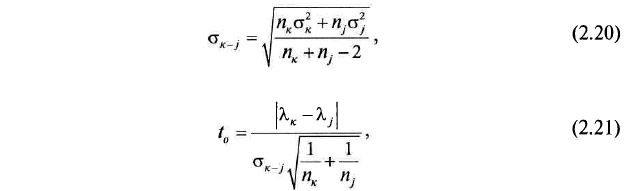
где σк и σj — среднеквадратические отклонения значений ламбда-критериев от средних для к-й и j-й точек кривой:
nк и nj — число оценочных блоков, использованных при расчетах средних значений критериев в к-й и j-й точках кривой;
λк и λj — средние значения ламбда-критериев для к-й и j-й точек кривой.
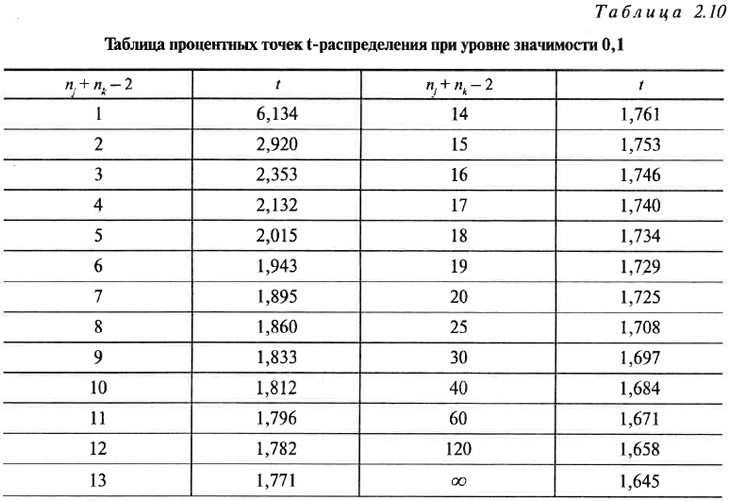
Если t0 меньше, чем величина t, определенная по известной табл. 2.10, то делается вывод о равенстве рассматриваемых средних значений λк и λj.

Из таблицы 2.10 при nj + nк — 2 = 39, следует, что значение t = 1,68. Поскольку t0 < t, то необходимо сделать вывод о статистическом равенстве значений λк и λj.
В-третьих, условие 2,в из табл. 2.9 может возникнуть не только при ограниченной возможности интерполяции, но и при существенной переразведке объекта, т. е. в условиях повсеместной правомерности интерполяции отметок (практически данная возможность реализуется чрезвычайно редко). Предварительно действие последнего обстоятельства может быть обнаружено по уровню значений ламбда-критериев. Если он не превышает 3—4 м для объектов I группы и 6—7 м для объектов II группы сложности геологического строения, то наиболее вероятна переразведка объекта. Для окончательного разрешения вопроса целесообразно дополнительно провести два дополнительных разрежения сети замеров и использовать для дальнейшего анализа полученную кривую разведанности.
Кривые разведанности, помимо их использования для оценки правомерности расчета ламбда-критериев, могут применяться и для сравнения геологической сложности объектов, находящихся на различных стадиях геологического изучения.
Например, при рассмотрении геологических материалов двух близрасположенных альтернативных участков для строительства шахты (шахта № 3 Менчерепского угледобывающего комплекса и шахта «Восточная») первый из них выглядел в части выдержанности гипсометрии и степени дизъюнктивной нарушенности явно предпочтительнее второго.
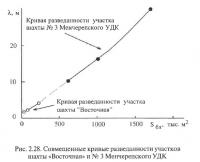
Однако, поскольку геологоразведочные работы по первому участку I находились лишь на стадии детальных поисков, а по второму — уже на стадии детальной разведки, данные которых обладают существенно различной степенью достоверности, простое сравнение их гипсометрических планов является явно некорректным. Для того чтобы учесть при принятии инвестиционного решения различие в степени геологической изученности участков, в единой системе координат были построены их кривые разведанности (рис. 2.28).
Из анализа рис. 2.28 следует, что кривая разведанности для шахты «Восточная» является простым продолжением кривой для шахты № 3 и, следовательно, оба объекта в действительности обладают практически равной сложностью поведения гипсометрии.
Таким образом, наблюдаемая более высокая сложность строения поля ш. «Восточная» является мнимой и обусловлена не природными свойствами данного объекта, а лишь более высокой степенью их изучения.
Заметим, что если бы совмещенные кривые разведанности этих участков имели бы вид, приведенный на рис. 2.29, то следовало бы сделать вывод о действительно более низкой сложности строения менее разведанного объекта.