Под рациональным сечением изолиний признака понимается сечение, обеспечивающее их построение с густотой, гарантирующей правомерность последующего выполнения линейной интерполяции между ними.
В настоящее время существует несколько методик выбора сечения.
В соответствии с предложением Г. И. Вилесова [9], изолинии должны отстраиваться при таком сечении, которое обеспечивает среднее расстояние между изолиниями на плане 5—10 мм (вне зависимости от масштаба плана и практически вне зависимости от сложности геометризируемой поверхности топофункции признака). Такая плотность изолиний почти всегда гарантирует весьма точное изображение топо-поверхности (при реально используемых масштабах 1:2000 и 1:5000), но требует значительных трудозатрат и является, как правило, избыточной.
Второй распространенный подход состоит в определении сечения изолиний h, исходя из неравенства:
где t — квантиль закона распределения ошибок показателя (обычно принимается равным 2);
σ — мера случайности в размещении показателя.
Величина определяется для линий замеров по формуле:
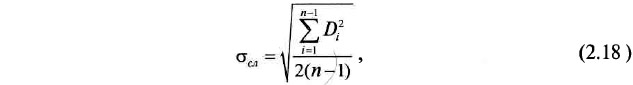
где Di = Рi — Рi+1 — значение разности между двумя соседними замерами;
n — число замеров в линии.
Несмотря на общепринятость рекомендаций по использованию соотношения 2.17, имеются сомнения в целесообразности их принятия. Для того чтобы разобраться в причинах этих сомнений, попытаемся ответить на несколько вопросов. Во-первых, для каких целей создается модель? Для того, чтобы впоследствии иметь возможность прогнозировать значение признака (точнее детерминированную составляющую его изменения) в любой точке пласта. Во-вторых, каким образом осуществляется это прогнозирование? Путем линейной интерполяции между изолиниями. От каких факторов зависит точность прогнозирования? От точности определения детерминированной и величины случайной составляющей изменчивости. Зависит ли точность определения детерми-пированной составляющей от величины сечения изолиний? Да, зависит: чем меньше сечение, тем меньше погрешность интерполяции. Зависит ли величина случайной составляющей от величины сечения изолиний? Такой зависимости быть не может.
Отсюда, по-видимому, можно сделать вывод о том, что в неравенстве 2.17 сравниваются абсолютно различные по смыслу данные. Величина, полученная из формулы 2.17, это не сечение, а своего рода доверительный интервал положения изолиний. Принятие его в качестве сечения может привести к неоправданному росту погрешности определения детерминированной составляющей, которого легко можно было бы избежать, взяв меньшее сечение. Кроме того, использование для расчета σсл формулы 2.17 может приводить к уменьшению сечения изолиний относительно необходимого, а следовательно, к росту трудозатрат. Это будет происходить, когда детерминированная составляющая описывается плоскостью или близкой к ней поверхностью.
Наиболее простой практический прием выбора сечения изолиний состоит в следующем. Выбирается какое-либо сечение, значение которого априорно превышает необходимое (например, такое, при котором по участку могут быть построены только 2—3 изолинии). Производится построение изолиний. Затем сечение уменьшается в два раза, и отстраиваются новые изолинии. Этот цикл операций повторяется до тех пор, пока вновь отстраиваемые изолинии не будут лежать практически на середине между уже построенными. Это значит, что произведено избыточное сгущение изолиний и вновь отстроенные линии излишни, так как не изменяют результаты прогнозирования с помощью модели. Например, пусть последовательно строились изогипсы с сечениями 100, 50 и 25 м. Причем изолинии при сечении 25 м находятся посредине между изогипсами, построенными при сечении 50 м. Следовательно, при графическом изображении рассматриваемой поверхности необходимо и достаточно изобразить на плане только изолинии с сечением 50 м. Описанный подход прост и доступен, однако требует выполнения значительного объема специальных, весьма трудоемких и квалифицированных построений.
Поэтому проще на основании описанной ниже математической процедуры реализовать данный подход не в графической, а в числовой форме.
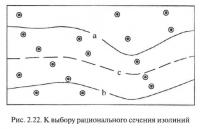
Основная идея этой процедуры совпадает с вышеописанной и состоит в следующем. Пусть по участку уже построены изолинии a и b с рациональным сечением h (рис. 2.22). Тогда промежуточная линия с=(a+b)/2 проходит, естественно, через середины расстояний между ними, а следовательно, площади, оконтуренные изолиниями a и c, c и b равны между собой. В этом случае, исходя из геометрического понятия вероятностей, можно утверждать, что в случае близкого к равномерному распределению скважин по площади участка должно иметь место равенство вероятностей попадания скважин в контуры ac и bc. Исходя из выполнения этого равенства для отдельной пары изолиний, можно говорить и об одинаковом законе распределения числа точек, попавших в левые (ac) и правые (bc) части интервалов, а также в сами интервалы (ab), на которые может быть разделена вся совокупность выполненных измерений. Оценка степени близости законов распределений по левым и правым частям интервалов к распределению по самим интервалам может быть произведена с помощью критерия λ А. Н. Колмогорова:
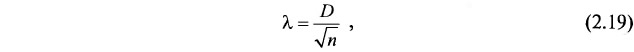
где D — максимум модуля разности накопленных эмпирических и теоретических частот;
n — общее число наблюдений в эмпирическом распределении.
Определение D ведется в табл. 2.8.
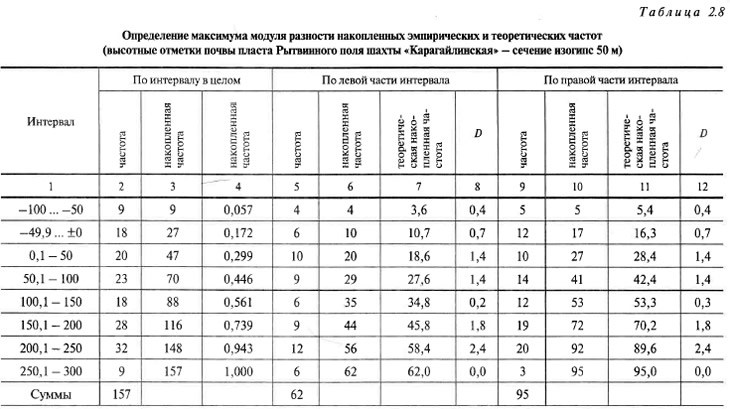
Во-первых, задается исследуемое значение сечения изогипс — интервал (50 м в табл. 2.8) и считается число замеров, попавших в каждый интервал (колонка 2), в его левую (колонка 5) и правую (колонка 9) части. В данном фактическом примере высотную отметку пласта в пределах от гор. —100 м до гор. —50 м имеют 9 подсечений (колонка 2), из них от гор. —100 м до гор. —75 м — 4 (левая часть интервала — колонка 5), а от гор. —75,1 м до гор. —50 м — 5 (правая часть интервала — колонка 9). Ясно, что сумма чисел по строкам, принадлежащим колонкам 5 и 9, равно числу в строке колонки 2 (4 + 5 = 9).
Во-вторых, находятся накопленные частоты (колонки 3, 6 и 10). Значение накопленной частоты по интервалу равно сумме частот данного и всех предшествующих ему интервалов.
В-третьих, рассчитываются накопленные теоретические частоты (колонка 4), путем деления чисел в строках колонки 3 на общее количество измерений (для первой строки таблицы: 9 / 157 = 0,057).
В-четвертых, заполняются колонки 7 и 11 путем умножения колонки 4, соответственно на суммы частот по колонкам 5 и 9 (для первой строки таблицы: 0,057 х 62 = 3,6 и 0,057 х 95 = 5,4).
В-пятых, находятся разности D. В колонке 8 записываются взятые по абсолютной величине разности чисел в колонках 6 и 7, а в колонке 12 — 10 и 11.
И наконец, в-шестых, находятся максимальные значения D. Для левой и правой половины интервала они равны 2,4. Затем по формуле 2.19 определяются значения критериев А. Н. Колмогорова для левой (λл = 2,4/620,5 = 0,30) и правой (λп = 2,4/950,5 = 0,25) части интервалов. В дальнейшем используется только максимальное значение критерия λ = 0,30.
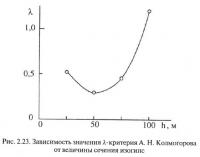
Расчет λ-критерия А. Н. Колмогорова производится несколько раз при различных задаваемых вариантах возможного сечения изогипс. После этого строится график зависимости λ-критерия А. Н. Колмогорова от величины рассматриваемого сечения (рис. 2.23). По графику определяется рациональное сечение изогипс, соответствующее минимуму λ (50 м на рис. 2.23), т. е. в наибольшей степени отвечающее сформулированному условию их рациональности. Фактически гипсометрический план пласта Рытвинного построен при сечении изогипс 100 м и, следовательно, требует производства дополнительных работ по их сгущению. При построении графика следует иметь в виду, что исследование функции h=f(λ) должно производиться начиная с больших сечений. Дело в том, что зависимость между сечением и λ при очень малых сечениях теряет устойчивость, после чего следует катастрофа (в математическом смысле).
Поэтому при начале перебора с малых сечений за отыскиваемый экстремум может быть ошибочно принят локальный экстремум участка потери устойчивости. Если при построении графика все λ больше 0,8 (что соответствует доверительной вероятности 0,54), то следует тщательно изучить вопрос о правомерности интерполяции между замерами, поскольку она в этом случае весьма сомнительна.