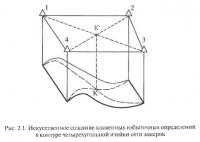
Неоднозначность построений может быть оценена лить при наличии избыточных измерений или определений. Однако в геологоразведочной практике они возникают крайне редко и нежелательны, т. к. являются следствием переразведки объекта исследований. Поэтому подход к созданию метода измерения степени неоднозначности модели может основываться только на выдвигаемой идее искусственного создания косвенных избыточных определений. Реализовать такую идею в условиях оговоренной конфигурации сети замеров можно в пределах четырехугольной ячейки сети замеров следующим образом [62].
Рассмотрим выпуклый четырехугольник с вершинами — точками замеров изучаемого признака (рис. 2.1). Присвоим его вершинам условные номера (от 1 до 4), начиная с произвольной вершины и увеличивая их по мере обхода четырехугольника по (или против) направлению движения часовой стрелки. В таком четырехугольнике можно провести две диагонали (1-3 и 2-4), пересекающиеся в точке К. Изучаемый признак Р, в соответствии со свойством однозначности геополя, должен иметь в точке К одно-единственное значение. Используя некоторый метод интерполирования, можно определить значение признака в точке К из каждой диагонали (Р1-3 — из интерполирования вдоль диагонали 1-3 и Р2-4 — из интерполирования вдоль диагонали 2-4). Ясно, что теоретически Р1-3 = Р2-4. Однако, в силу наличия погрешностей измерений и интерполяции, значения Р1-3 и Р2-4 не будут совпадать. Поэтому разность Р1-3 и Р2-4, являясь разностью двух независимых косвенных определений, может рассматриваться в качестве численной меры неоднозначности построений.
Таким образом, критерий достоверности изучения признака в контуре четырехугольника сети измерений может быть определен выражением:
Предлагаемый подход, имея совершенно иное теоретическое обоснование, внешне — прежде всего в части формы оценочного блока (четырехугольника сети измерений) — напоминает подход А. И. Осецкого [30]. Поэтому следует особо выделить элементы, отличающие «красные числа» А. И. Осецкого от критерия Ккр:
- критерий А. И. Осецкого ориентирован на оценку точности определения только объема полезного ископаемого, а Ккр — на оценку неоднозначности геометрической модели;
- «красные числа» определяются исключительно на основе применения линейной интерполяции между замерами;
- форма ячейки сети полагается исключительно правильной — квадратом, ромбом, прямоугольником, т. е. предполагает идеализацию реального характера размещения точек сети измерений.
С помощью критерия Ккр возможна оценка неоднозначности модели любого количественно определяемого признака. Метод интерполяции, используемый при расчетах критериев Ккр, должен по точности соответствовать методу, использованному при построении модели размещения признака. Однако возможно применение критерия и в случае, когда эти методы существенно различны по точности, но известно соотношение их погрешностей f:
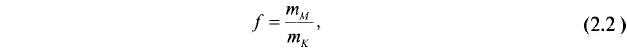
где mм — погрешность метода, использованного при построении модели; mк — погрешность метода интерполяции, примененного при расчете критерия Ккр.
Зная f, можно откорректировать рассчитанные значения критериев так, чтобы они отражали точность фактически используемого метода построения модели:
Естественно, что формула 2.3 получена из весьма вероятного допущения о том, что отношение погрешностей методов интерполяции равно отношению степеней неоднозначностей построенных с их помощью геометрических моделей.
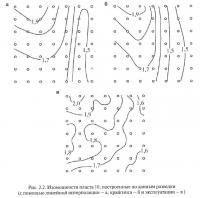
Расчет погрешностей mм и mк имеет научно-исследовательский характер, разово выполняется на стадии апробации нового метода моделирования и производится на основе сравнения данных разведки и эксплуатации с последующим распространением результатов на аналогичные геологические образования. Например, на рис. 2.2 приведен фрагмент трех вариантов плана изомощностей пласта 10 (поле шахты «Пионерка»), построенных по данным скважинных измерений с применением линейной интерполяции (рис. 2.2, а) и точечного крайгинга (рис. 2.2, б), а также по данным горных работ (рис. 2.2,в). Предположим, что итоговую модель изомощностей предполагается строить с помощью крайгинга, а расчет критериев Ккр — с помощью линейной интерполяции. Для определения погрешностей mм и mк на планы накладывается одна и та же квадратная сетка узлов (положение каждого узла обозначено на рис. 2.2 окружностью) с расстоянием между узлами 50 м. Общее число узлов не должно быть менее 30. В каждом узле сетки определяются три значения признака: по данным интерполяции, с помощью которой рассчитываются критерии (в примере — линейной — Pкi), по данным интерполяции, использованной при построении модели (в примере — крайгинга — Pмi) и горных работ (Pгi). Результаты определений заносятся в табл. 2.1, в которой в колонки 5 и 7 записываются вычисленные разности данных горных работ и данных, полученных с помощью различных методов интерполяции, а в колонках 6 и 7 — соответственно их квадраты. Затем определяются суммы и среднеарифметические значения чисел по колонкам 6—8 (строки «Сумма» и «Среднее»). Их буквенные обозначения приведены в табл. 2.1.
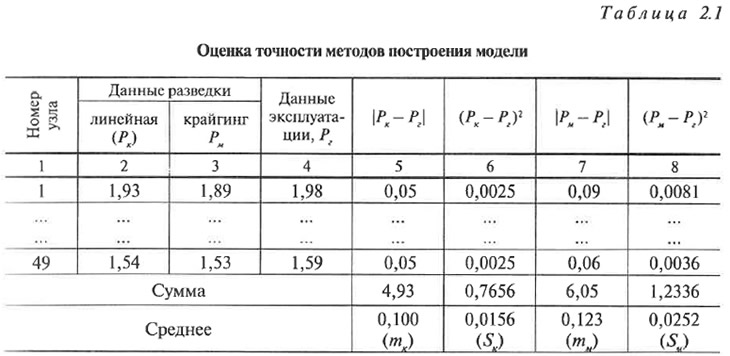
Естественно, что mк характеризует погрешность метода интерполяции, примененного при расчете критерия Ккр, а mм — погрешность модели. Однако поскольку значения mк и mм определяются по конечному числу наблюдений, то различие в их значениях может быть связано со случайными причинами, т. е. статистически они могут рассматриваться как одинаковые и коэффициент пересчета f следует принимать равным единице. Поэтому перед вычислением f проверяется гипотеза о равенстве значений средних погрешностей mк и mм.
Учитывая, что число узлов n постоянно для обоих сопоставляемых методов интерполяции, применяемый статистический критерий Z pacсчитывается по формуле:
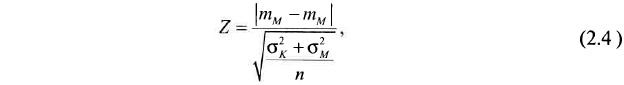
где σк — среднеквадратическое отклонение разностей фактических и расчетных значений признака в узлах при использовании метода интерполяции, применяемого при вычислениях критериев разведанности;
σм — среднеквадратическое отклонение разностей фактических и расчетных значений признака в узлах при использовании метода интерполяции, применяемого при создании геометрической модели.
Значение а удобно рассчитывать по известной формуле:
Для условий рассматриваемого примера значения среднеквадратических отклонений составляют:
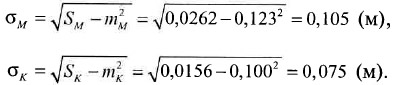
Следовательно:
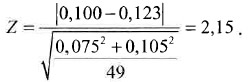
Если значение Z превышает величину 1,64, то с вероятностью 0,95 можно утверждать, что погрешности обоих рассматриваемых методов интерполяции равны друг другу. Отсюда, для условий примера, можно утверждать, что модели пространственного размещения мощности угольного пласта, выполненные с помощью точечного крайгинга и линейной интерполяции, равноточны. В силу этого коэффициент /равен единице, а критерии разведанности, рассчитанные с помощью линейной интерполяции, вполне применимы для оценки однозначности модели, построенной методами точечного крайгинга.
Аналогичные исследования, проведенные при изучении точности изучения зольности пласта Поленовского, также продемонстрировали статистическую равноточность линейной интерполяции (средняя погрешность 3,9 % в абсолютных единицах измерения зольности) и крайгинга (средняя погрешность 3,0 %).
Отметим, что вывод о равноточности крайгинга и традиционных моделей в условиях угольных месторождений не является новым. К аналогичным выводам ранее пришли исследователи США [64] и Германии [68]. По-видимому, данное обстоятельство связано с особенностями строения угольных пластов, представляющих собой суперпозицию отдельных угольных линз [66] и, как следствие, в принципе не обеспечивающих процедуры крайгинга необходимым количеством наблюдений в пределах отдельных однородных угольных образований (порядка 400 [67] — 1000 [69] пар замеров для построения исходной полувариограммы).
Помимо правильной сетки, при оценке погрешностей mк и mм может применяться нерегулярная сетка узлов. В ее качестве используются имеющиеся точки замеров значений геометризируемого признака в горных выработках (места производства маркшейдерских замеров, геологических зарисовок, отбора проб). В этом случае отпадает необходимость в предварительном построении фактической топоповерхности изучаемого признака. Однако при использовании этого подхода необходимо обеспечить хотя бы приближенную статистическую равномерность размещения узлов нерегулярной сетки по площади участка сопоставления данных.
Таким образом, предлагаемый подход к дифференциальной оценке неоднозначности геометрических моделей, основанный на создании косвенных избыточных определений в четырехугольнике сети замеров путем интерполяции значений признака вдоль его диагоналей, применим и в случае, когда собственно процесс моделирования не предполагает производства интерполирования между отдельными парами замеров и производится методами крайгинга, аппроксимацией различными аналитическими функциями, методом блуждающего окна и т. д.