Предпосылкой к использованию метода в этих целях является наличие тесной корреляционной связи между значениями ламбда-критериев разведанности и амплитудами нарушений, попадающих в четырехугольники сети скважин (рис. 3.15). Отсюда следует, что можно прогнозировать дизъюнктивные дислокации по признаку резкого увеличения величины ламбда-критерия разведанности в отдельных оценочных блоках или их группах.
Однако визуально фиксируемая аномальность критериев отмечается только в случае встречи разрывов достаточно больших амплитуд, которые в своем подавляющем большинстве или непосредственно подсекаются скважинами, или надежно фиксируются методом структурных построений. Кроме того, при таком подходе трудно локализовать место расположения нарушения, его ориентировку и протяженность. Поэтому возникает задача перехода от оценок по блокам к оценкам по районам отдельных скважин.
Напомним, что значения ламбда-критериев обусловлены действием трех основных факторов:
- техническими погрешностями измерений и определений данных по пластоподсечениям;
- погрешностями применяемого метода интерполирования (метода построения модели гипсометрии);
- погрешностями построений, связанными с наличием установленных или невыявленных тектонических нарушений.
Отсюда следует, что значения поправок εi к высотным отметкам также должны быть связаны с этими же факторами. Причем поправки характеризуют уже окрестности конкретных замеров, а не отдельные изолированные оценочные блоки.
К сожалению, перечисленные факторы действуют одновременно, тогда как с позиции прогнозирования необходимо оценить лишь влияние последнего из них. В основу процесса такой оценки может быть положено достаточно естественное предположение о том, что технические погрешности измерений (зависящие от использованных технических методов измерений) и погрешности интерполирования (зависящие от плотности разведочной сети и сложности геологического строения) в условиях отдельного конкретного объекта носят характер своеобразного «информационного шума», действуют повсеместно и относительно постоянны. В это же время погрешности построений, связанные с тектоническими нарушениями, проявляются лишь на локальных участках, переменны по величине, т. е. образуют отдельную статистическую совокупность.
Выделение «шумовой составляющей» предлагается осуществлять на основе анализа интенсивности изменения значений поправок между соседними точками измерений. Числовой характеристикой этого изменения является градиент поправок:
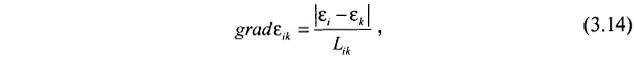
где εi и εk — значения поправок для i-го и k-го соседних замеров;
Lik — расстояние между i-м и k-м соседними замерами.
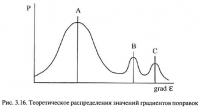
Так как приращение поправок, связанное с действием двух первых факторов, не должно быть значительным, то и обусловленные ими величины градиентов не должны претерпевать больших изменений, характеризуясь некоторым ожидаемым средним значением и дисперсией. Распределение таких градиентов (которые будем в дальнейшем называть «нормальными», в силу порождающих их явлений) теоретически должно подчиняться нормальному закону (распределение А на рис. 3.16).
Градиенты, связанные с наличием дизъюнктивных нарушений (в дальнейшем — «аномальные» градиенты), также должны образовывать собственные законы распределения, отличающиеся своим математическим ожиданием и дисперсией. При наличии нескольких групп геометрически однотипных разрывов могут образовываться несколько распределений аномальных градиентов (распределения В и С на рис. 3.16).
Таким образом, практически распределение градиентов должно представлять собой суперпозицию нескольких законов распределения, что многократно подтверждалось в ходе практического применения метода (см., например, рис. 3.17).
Таким образом, первой задачей прогнозирования является расчет градиентов поправок и построение гистограммы их распределения. Главной проблемой при этом является установление рационального числа количества интервалов гистограммы. Например, на рис. 3.18 приведены гистограммы распределения одних и тех же градиентов поправок, построенные при различном принятом числе интервалов. Из рисунка наглядно видно, насколько сильно их количество изменяет характер гистограммы.
Большинство авторов [5; 8; 9; 11; 13; 26 и др.] рекомендуют производить выбор величины интервала (класса) Δh по формуле:
где hmax — максимальное значение признака;
hmin — минимальное значение признака;
К — число интервалов.
Известны также предложения, состоящие в выборе величины интервала равной удвоенной или утроенной погрешности измерений. Однако они полностью неприменимы в рассматриваемом случае, поскольку градиенты поправок не являются измеренными величинами.
Наибольшие расхождения во мнениях наблюдаются при решении вопроса о выборе числа интервалов К. Многие авторы [5; 9; 11 и др.] рекомендуют использовать для этой цели формулу Стерджесса:
где N — число обрабатываемых наблюдений.
А. К. Митропольский [26] рекомендует, вне зависимости от числа наблюдений, всегда принимать число интервалов равным 12, а А. М. Длин — 7,9 или 11 [13], но сама величина интервала не должна быть при этом меньше цены деления измерительною прибора. Е. С. Вентцель предлагает разделять размах на 10—20 интервалов [8]. Перечень этих весьма различных предложений можно легко продолжить.
Таким образом, возникает задача отыскания оптимальной величины интервала. Ее решение предполагает прежде всего получить ответ на вопрос: какую величину целесообразно отыскивать — число интервалов или их величину? Поставим для этого умозрительный эксперимент: пусть имеется выборка из 200 замеров, например, мощности пласта энергетического угля (кондиционная мощность которого составляет 1 м). Причем в 100 из них мощность пласта меньше 1 м, а в остальных больше. Если задаться целью построить гистограмму распределения признака, то число интервалов (по Стерджессу) составит 8·(l + 3,2 lg200). Теперь представим себе, что необходимы гистограммы распределения отдельно для кондиционных и некондиционных мощностей. Каждая из них должна состоять из 7·(1 + 3,2 lg100) интервалов. Следовательно, в этом случае весь диапазон изменения мощностей будет разделен уже на 14, а не на 8 частей. Налицо явное противоречие. Оно возникает и при использовании любого другого из рассмотренных способов.
Разрешить это противоречие можно двумя путями:
- принять нелинейную зависимость между числом интервалов и числом измерений;
- отыскивать не оптимальное число интервалов, а их оптимальную величину.
Первый путь выглядит бесперспективным. Во-первых, весь многолетний опыт практической статистики не указывает на возможность существования такой формы связи. Во-вторых, для того чтобы сформировать обучающую выборку для установления такой связи, необходимо для каждого числа измерений найти оптимальное число интервалов, т. е. предварительно решить рассматриваемую задачу. И в-третьих, зависимость числа интервалов от объема выборки должна обусловливаться видом распределения. Например, для равномерного закона распределения будет, по-видимому, существовать достаточно широкий диапазон возможного числа интервалов, обеспечивающего представительность гистограммы, в то время как для полимодальных распределений этот диапазон достаточно узок (см. рис. 3.18).
Поэтому первый путь решения задачи построения оптимальной гистограммы является лишь частным случаем второго пути. Отсюда следует, что целесообразно ориентироваться на непосредственный поиск величины интервала для каждой конкретной гистограммы.
Априорно ясно, что интервал гистограммы не должен быть слишком велик (при его величине, равной размаху выборки, любое распределение станет равномерным) или слишком мал (при его величине, меньшей точности записи чисел, любое распределение также будет сводиться к равномерному).
А. М. Длин считает, что «ширина интервала должна способствовать выявлению основных черт распределения и сглаживанию случайных колебаний. При этом нужно учесть, что случайные колебания будут преобладать в малом интервале, так как в нем заключено меньшее число наблюдений, чем в большом [13, с. 53]. Исходя из боязни допустить значимые случайные колебания гистограммы, им и предложено весьма небольшое количество интервалов, максимальное число которых практически совпадает с их минимальным количеством, рекомендуемым Е. С. Вентцель. Последняя более диалектична и обращает внимание не только на нежелательность больших, но и малых интервалов. «Число разрядов, на которые следует группировать статистический материал, не должно быть слишком большим (тогда ряд распределения становится невыразительным и частоты в нем обнаруживают незакономерные колебания); с другой стороны, оно не должно быть слишком малым (при малом числе разрядов свойства распределения описываются статистическим рядом слишком грубо)» [8, с. 137].
Таким образом, оптимальный интервал должен обеспечивать определенный баланс между уровнем незакономерных колебаний частот и уровнем подробности вскрытия свойств распределения.
Рассмотрим, какой интервал наиболее приемлем с позиции изучения подробностей свойств распределения. Очевидно, что им является интервал, стремящийся к нулю. В этом случае будет обеспечиваться минимальная разность частостей, попавших в соседние интервалы наблюдений, т. е. максимальная подробность гистограммы. Степень этой «подробности» для каждой рассматриваемой величины интервала может быть охарактеризована величиной
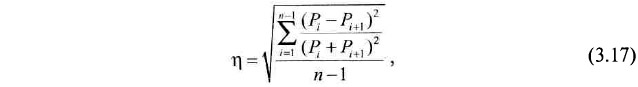
где n — число интервалов;
Рi — частота в i-м интервале.
Легко заметить, что параметр η характеризует среднеквадратическое отклонение частостей соседних интервалов гистограммы, выраженных в относительной мере.
С позиции уровня нежелательных незакономерных колебаний частостей целесообразно также минимизировать изменение частостей соседних интервалов, т. е. обеспечить выполнение условия:
Пользуясь формулой 3.17, можно для каждого наперед заданного интервала Ah рассчитать и построить зависимость η = f(Δh). Интервал, соответствующий условию 3.18, является наилучшим, т. к. обеспечивает минимизацию незакономерных колебаний при максимальной подробности гистограммы.
В качестве примера на рис. 3.19 приведены экспериментальные зависимости η = f(Δh). Формы зависимостей достаточно характерны и проявляются не только при исследовании распределений градиентов поправок, но и различных горно-геометрических характеристик [48J. Их характер полностью соответствует теоретическим представлениям теории катастроф [10]. Поскольку не существует предварительных соображений относительно вида уравнения, надлежащим образом описывающего рассматриваемую систему взаимодействия параметров, то распознавание катастроф осуществляется на основе выявления их «флагов». Приведенная на рис. 3.19 зависимость имеет на участке АВ «флаги»:
- модальности (функция имеет более одного локального минимума);
- недостижимости (имеет седло неустойчивого равновесия);
- катастрофических скачков (малые изменения в значениях управляющего параметра Ah вызывают большие изменения в состоянии системы);
- расходимости (конечные изменения в значении управляющего параметра приводят к конечным изменениям переменной в точке равновесия.
Характер «флага» катастрофических скачков и отсутствие «флага» гистерезиса на участке АВ указывают на необходимость применения к процессу принципа Максвелла. В соответствии с ним система выходит из одного состояния метастабильного равновесия и начинает двигаться к другому метастабильному равновесию или устойчивому равновесию в зависимости от уровня шума в системе. На участке ВС «флагов» нет, и, следовательно, он является участком устойчивости.
Исходя из высказанных соображений, поиск оптимального интервала должен начинаться с заведомо больших интервалов и завершаться после нахождения первого минимума зависимости. В противном случае результаты могут быть искажены постоянно возрастающими шумами.
Практически суммирование при вычислении η производится только до первой пары интервалов, суммарно содержащих менее 5 % наблюдений (обычно одним из них является интервал, не содержащий ни одного градиента).
Наличие таких пар вносит существенные искажения в результаты расчетов (происходит переход к совместному рассмотрению двух независимых гистограмм) и приводит (в случае двух соседних «пустых» интервалов) к делению на ноль. Такой подход не противоречит сложившейся практике, требующей предварительного исключения аномалий.
Средством автоматизации процесса прогноза является программа «PDD». В качестве исходных данных программа использует файлы данных и квадриангулирования, формируемые программой «DRU». После производства уравнивания пользователь получает возможность ознакомиться со значениями полученных поправок. Они используются в двух направлениях.
Во-первых, исходные данные по замерам, обладающим значительными поправками, должны подвергаться сомнению на предмет наличия в них грубых ошибок, допущенных в ходе документирования результатов разведки или сбора материалов. Рекомендуется производить повторную перепроверку введенных в компьютер данных по таким замерам.
Во-вторых, в некоторых случаях, о которых будет сказано ниже, поправки используются для последующего построения изолиний поправок к высотным отметкам.
Градиенты поправок рассчитываются программой автоматически. В качестве направлений, по которым они вычисляются, используются четыре стороны и две диагонали каждого четырехугольника. Естественно, что каждое рассматриваемое направление используется всего один раз. Для этого программой постоянно проверяется: не было ли вновь намеченное направление ранее использовано.
Следующий режим программы обеспечивает построение гистограммы градиентов поправок. Режим реализован в интерактивном виде: пользователь задает возможное число интервалов, а программа сообщает ему значение показателя изменчивости η и показывает вид гистограммы (рис. 3.20).
После построения оптимальной гистограммы (по условию 3.18) выбирается первый интервал аномальных значений градиентов. Для облегчения его поиска автоматически осуществляется декомпозиция экспериментального закона распределения путем выделения распределений нормальных и аномальных градиентов поправок (последнее показано на рис. 3.20 штриховкой).
Выбор первого аномального интервала осуществляется визуально. В его качестве принимается интервал, для которого доля аномальных градиентов превышает 70 % (на рис. 3.20 за такой интервал должен быть принят пятый интервал). Относительно его начального значения все градиенты делятся на аномальные и нормальные. Направления аномальных градиентов прочерчиваются на плане и рассматриваются как направления, пересеченные разрывными нарушениями. В программе «PDD» это прочерчивание выполняется автоматически (рис. 3.21).
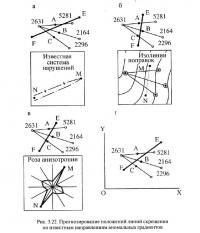
На следующем этапе прогнозирования намечаются положения вероятных линий скрещения (утолщенные линии на рис. 3.21). Они проводятся под условием пересечения ими линий аномальных градиентов. Само построение выполняется одним из четырех способов.
Первый из них состоит в учете ориентировки известных систем разрывных нарушений (рис. 3.22, а). В этом случае все линии градиентов делятся пополам (намечаются точки А, В и С). Затем проводится прогнозируемая линия скрещения FE таким образом, чтобы она была параллельна линиям скрещения известных нарушений NM и пересекала все линии аномальных градиентов, причем, по возможности, проходя в максимальной близости от срединных точек А, В и С (последнее условие должно выполняться для всех способов трассировки).
Второй и третий способы состоят в учете направлений изолиний поправок. Смысл учета состоит в том, что если ожидается пересечение нарушениями направлений максимального изменения значений поправок (которыми, естественно, являются направления падения поверхности поправок), то линии скрещения должны быть параллельны изолиниям поправок.
Учет ориентировки изолиний выполняется либо путем проведения линии скрещения FE параллельно ближайшим изолиниям поправок (направлению NMна рис. 3.22, б) — второй способ, либо параллельно главной оси розы анизотропии поправок, отражающей преимущественную ориентировку изолиний поправок по участку (направлению NM на рис. 3.22, в) — третий способ. Причем использование розы анизотропии допустимо только в случае наличия ярко выраженных осей анизотропии. Методика построения розы анизотропии (которая автоматически отстраивается программой «PDD») будет рассмотрена несколько ниже.
Четвертый способ (рис. 3.22, г) применяется при хаотичном изменении поправок, что встречается крайне редко. При его использовании вводится произвольная система координат YOX. Далее, рассматривая срединные точки А, В и С в качестве своеобразных точек наблюдений, предполагаемая линия скрещения проводится путем линейной аппроксимации полученной «зависимости» с помощью метода наименьших квадратов. Естественно, что все описанные действия на практике производятся интерактивно.
Приведенные на рис. 3.22 методы трассировки нарушений размещены в порядке убывания степени предпочтительности их применения, т. е. вариант трассировки по схеме рис. 3.22, а предпочтительнее варианта рис. 3.22, б и т. д.
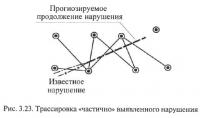
На практике встречается также простейший случай трассировки, состоящий в простом продлении выявленного геологоразведочными или горными работами нарушения (рис. 3.23).
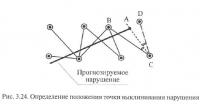
Ожидаемую точку выклинивания дизъюнктива («окончание» линии скрещения — точка А на рис. 3.24) рекомендуется располагать на середине расстояния между последним аномальным (СВ) и ближайшим к нему нормальным градиентом (CD). Для этого угол между направлениями градиентов СВ и CD делится биссектрисой СА пополам и ранее намеченная линия скрещения продолжается до пересечения с ней в искомой точке А.
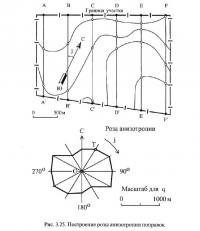
Упомянутая выше роза анизотропии строится по правилам, практически совпадающим с правилами построения индикатрис анизотропии поверхностей геополей [39]. Для этого на участок накладывается палетка в виде системы параллельных равноотстоящих линий, расстояние между которыми примерно равно среднему расстоянию между изолиниями. Первоначально ориентация линий палетки (А—А', В—В', ..., F—F' на рис. 3.25) принимается меридиональной. Производится измерение длин отрезков линий, попавших внутрь рассматриваемого участка (для рис. 3.25 это LA—A', LB—B', ..., LF—F'), и определяется их сумма:
Для изображенного на рис. 3.25 примера она равна 11160 м. Затем подсчитывается общее число пересечений изолиний с линиями палетки (N, в примере оно составляет 18) и рассчитывается параметр q, характеризующий среднее расстояние между изолиниями вдоль заданного направления (в данном случае — меридионального):
В рассматриваемом примере q =11160/18 = 620 м.
После этого палетка поворачивается на угол φ (принимаемый, обычно кратным 30°, т. е. вначале 30°, затем 60°, 90° и т. д.) и все вычисления повторяются вновь. В результате работы формируется табличная зависимость значений параметра q от величины угла φ (табл. 3.5).
Затем подготавливается основа розы анизотропии (индикатрисы), представляющая собой серию лучей, исходящих из общего центра О и ориентированных в соответствии с принятыми значениями углов φ. Вдоль каждого луча в принятом масштабе от центра О откладывается соответствующая углу φ величина q (например, для направления ОТ она равна 720 м). Полученные концевые точки (типа 7) соединяются между собой.

Поскольку вдоль преимущественного простирания изолиний расстояние между ними максимально, то направление максимального по длине луча розы анизотропии соответствует ожидаемой ориентировке прогнозируемых дизъюнктивных нарушений (для рис. 3.25 оно равно 120°).
Естественно, что для построения розы анизотропии должна использоваться геометрическая модель геополя поправок, построенная при постоянном сечении изолиний. Сама величина сечения не должна превышать оптимального уровня, устанавливаемого по правилам, изложенным в параграфе 3.4.
Для компьютерной обработки описанный подход построения розы мало пригоден из-за сложности его формализации. Поэтому в программе «PDD» используется нерегулярная цифровая модель поправок.
При этом по каждому i-му градиенту поправок gradεi рассчитывается его дирекционный угол αi и расстояние di, при котором должно происходить изменение поправок на величину в 1 м:
Далее градиенты объединяются в шесть близких по дирекционным углам групп:

Для каждой группы по всем вошедшим в нее градиентам определяется среднее значение параметров di — величина q (аналогичная по своему смыслу вычисляемой по формуле 3.20). Каждому значению q ставится в соответствие угол φ группы (для группы 1 он равен 0° и 180°; 2 — 30° и 210°; 3 — 60° и 240°; 4 — 90° и 270°; 5 — 120° и 300°; 6 — 150° и 330°), формируется таблица, аналогичная табл. 3.5, и выполняется построение розы анизотропии.
Практика применения обоих рассмотренных подходов к построению роз анизотропии поправок позволяет оценить их как равноправные.
Встречаются два основных вида роз анизотропии:
- с ярко выраженными осями анизотропии (например, рис. 3.21);
- с отсутствием явно выраженной анизотропии (рис. 3.25).
Ясно, что для прогноза положений нарушений может использоваться только первый тип роз. При получении розы второго типа необходимо произвести изучение анизотропии не только в целом по участку, но и по отдельным его частям, охватывающим район расположения рассматриваемой группы аномальных градиентов (возможность выполнения такого анализа заложена в программе «PDD»). В результате, как правило, достигается получение пригодной для использования при трассировке разрыва розы анизотропии первого типа (что избавляет пользователя от необходимости построения модели размещения значений поправок).
Важной составной частью процесса прогноза разрывных нарушений является прогноз их амплитуд. В результате статистической обработки экспериментальных материалов, учитывающей нарушения с амплитудами от 1 до 19 м, была разработана следующая методика прогноза вертикальных амплитуд смещений.
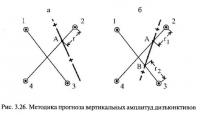
На первой стадии прогноза работа ведется по отдельным оценочным четырехугольникам. В случае если прогнозное нарушение пересекает одну диагональ оценочного блока (рис. 3.26, а), то определяется точка А пересечения диагонали и разрыва, находится ближайшая к ней вершина четырехугольника (2 на рисунке) и измеряется расстояние между ними r. Ожидаемая вертикальная амплитуда разрыва рассчитывается по формуле:
где λ — значение ламбда-критерия разведанности (если |λ| > 3 м, то в расчет принимается величина, равная |λ| — 1 м);
R — длина диагонали, пересекаемой нарушением.
В случае, если прогнозное нарушение пересекают обе диагонали (рис. 3.26, б), определяются две точки их пересечения с разрывом (А и В) и измеряется расстояние от них до ближайших к ним вершинам четырехугольника (r1 и r2). Ожидаемая вертикальная амплитуда разрыва оценивается по формуле:
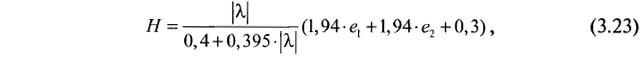
где e1 = r1/R1; e2 = r2/R2;
R1 и R2 — длины соответствующих диагоналей.
Если прогнозное нарушение пересекает диагонали нескольких четырехугольников, то расчет амплитуды производится по каждому из них, а в качестве ожидаемой ее величины принимается среднеарифметическое из полученных частных значений.
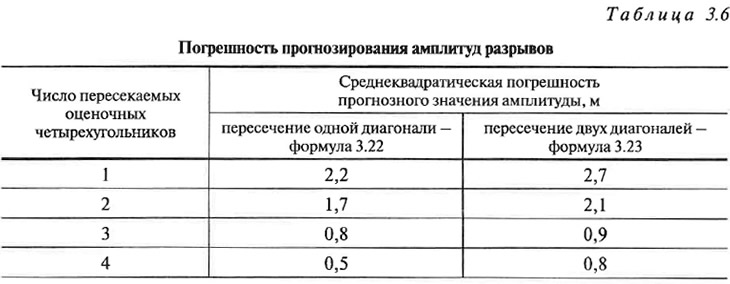
Экспериментально установленные погрешности прогнозных амплитуд разрывов приведены в табл. 3.6, из которой следует, что они с точки зрения их практического применения не зависят от количества пересекаемых дизъюнктивом диагоналей. Следовательно, в случае прохождения нарушения через несколько оценочных блоков с различным числом пересекаемых им диагоналей, в качестве ожидаемой амплитуды нарушения также правомерно принимать среднеарифметическое значение из отдельных «блоковых» амплитуд.
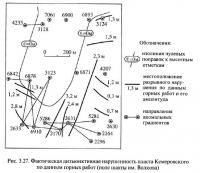
В качестве примера прогнозирования на рис. 3.27 приведены установленные горными работами нарушения пласта Кемеровского поля шахты им. Волкова с дополнительным нанесением изолинии поправок и линий аномальных поправок. Результаты прогнозирования их положения только по геологоразведочным данным были показаны на рис. 3.21.
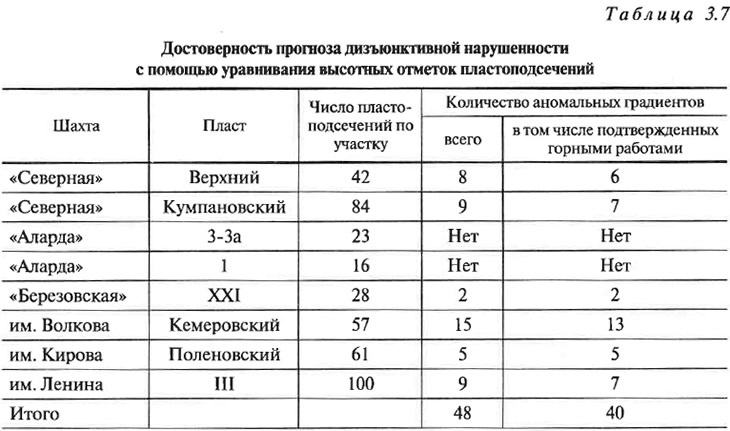
Результаты оценки точности прогнозирования дизъюнктивных нарушений, выполненной по геологоразведочным данным уже отработанных участков пластов, представлены в табл. 3.7. В целом из числа выделяемых аномальных градиентов примерно 80 % подтверждаются последующими горными работами. По приведенным в табл. 3.7 сопоставлениям методом уравнивания выявлялось от 50 до 80 % всех фактически имеющихся нарушений с амплитудами более 4 м, что в два-три раза превышает число нарушений, выявленных геологоразведочными работами.
Однако необходимым условием успешного применения метода является наличие качественных геологических данных, соответствующих вполне достижимым инструктивным требованиям. Вполне понятно, что невозможно достичь хороших результатов прогнозирования по фальсифицированным или недобросовестно полученным исходным материалам.
Например, в 1989 г. при применении рассматриваемого метода для прогноза нарушенности поля шахты «Полосухинская» были получены отрицательные результаты. В ходе анализа причин неэффективной работы метода вскрылись факты грубейших нарушений технологии геологоразведочных работ: более 60 % пластоподсечений, находящихся на уже отработанной площади, имели случайные погрешности высотных отметок, превышающие допуски технических требований. Более того, в 20 % скважин эти погрешности превышали 10 м, в том числе, например, и по пластоподсечению, залегающему на глубине всего 20 м!
Так как на практике, к сожалению, часто приходится работать с материалами подобного уровня, то в результате накопленного практического опыта удалось выработать некоторые методические рекомендации по их обработке.
Во-первых, если анализируется материал по частично отработанному пласту, то вначале рекомендуется провести обработку геологоразведочных данных уже отработанного контура, сопоставить результаты прогноза и эксплуатации и выявить амплитуды нарушений, действительно устанавливаемых с помощью уравнивания. После выполнения прогноза по не затронутой горными работами части пласта следует игнорировать прогнозные нарушения, амплитуды которых меньше обнаруживаемых. Естественно, что такой подход правомерен лишь в случае, если анализируемый и эталонный участок изучались в рамках одних и тех же стадий геологоразведочных работ.
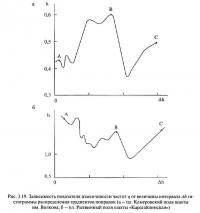
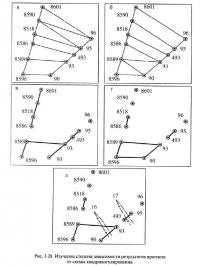
Во-вторых, необходимо изучать степень зависимости результатов прогноза от схемы квадриангулирования. Установлено, что наличие в исходных данных грубых ошибок приводит к неустойчивым прогнозным оценкам. Изучение производится с помощью выполнения не одного, а двух-трех различных вариантов квадриангулирования сети с последующим выявлением устойчивой группы аномальных градиентов. Например, на рис. 3.28,а и 3.28,б приведены фрагменты двух вариантов квадриангулирования разведочной сети по пласту Рытвинному поля шахты «Карагайлинская». Различная квадриангуляция приводит к выделению несколько различных аномальных градиентов (соответственно рис. 3.28,в и 3.28,г). Однако оба варианта прогноза имеют общие аномальные градиенты (рис. 3.28,д), которые и используются при выполнении окончательного прогноза. Ориентировка нарушений по розам анизотропии мало зависит от схемы квадриангулирования (в примере она неизменна и составляет 30°). На поле рис. 3.28,д в иллюстративных целях нанесены нарушения, выявленные геологоразведочными работами (отметим, что дизъюнктив № 16, вероятно, имеет более значительную протяженность, проходя между скважинами 8586 и 8518, и, кроме того, следует ожидать дополнительный разрыв, пересекающий направление 8589—8596). При наличии грубых погрешностей в исходных данных различные схемы квадриангуляции дают большие расхождения в результатах прогноза, что является своего рода «флагом катастрофы», сигналом о некорректности прогнозирования.
В-третьих, после завершения прогноза следует проанализировать амплитуды прогнозируемых нарушений. Те из них, амплитуды смещения которых составляют менее 70 % от величины среднего значения ламбда-критерия разведанности по участку, целесообразно отбрасывать, поскольку такие относительно незначимые аномалии могут быть обусловлены погрешностями измерений.
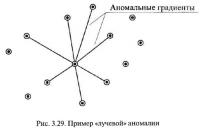
В-четвертых, предварительно следует отбраковывать и не интерпретировать как нарушения (если тому нет иных предпосылок) «лучевые» аномалии, когда из некоторого пластоподсечения исходит серия разнонаправленных аномальных градиентов (рис. 3.29). Это указывает на то, что замер со всех сторон как бы отсечен разрывными нарушениями, не фиксируемыми по иным направлениям. Вероятнее всего, что данные по такому замеру просто искажены. В этом случае требуется перепроверить их на предмет выявления грубых ошибок. Кроме того, в данной неопределенной ситуации необходимо осуществлять поиск признаков, косвенно подтверждающих наличие дизъюнктива.
В-пятых, аналогичный поиск целесообразно производить также и в случае появления одиночного аномального направления, так как его существование может быть связано с действием случайных факторов. Ошибочно аномальные градиенты могут возникать и в ходе декомпозиции общего закона распределения градиентов (например, на рис. 3.20 первый выделенный аномальный интервал, отмеченный маркером мыши, содержит не только аномальные градиенты, но и незначительную долю (менее 9 %) нормальных градиентов). Интерпретация одиночного градиента в качестве результата влияния нарушения должна производиться лишь в случае подтверждения его наличия косвенными признаками.
К ним можно отнести следующие.
Во-первых, наличие по участку выявленного нарушения, естественным продолжением которого является прогнозируемое (как в случае с дизъюнктивом № 16 на рис. 3.28).
Во-вторых, существование нарушения по выше- или нижележащим пластам, продолжением которого может являться прогнозируемое.
В-третьих, аномальные колебания в значениях углов напластования по окружающим скважинам. Например, при прогнозе нарушений по пласту Алчедатскому III прогнозировалось нарушение, не зафиксированное геологоразведочными работами. При анализе материалов геологических разрезов по скважине 5074 (рис. 3.30,а) отмечено аномальное изменение угла напластования (аномальная зона помечена знаком вопроса). При рассмотрении ее как зоны возможного нахождения дизъюнктива и последующем его проведении параллельно уже известным разрывам его пересечение с пластом Алчедатским III должно происходить в районе, близком к району, прогнозируемому с помощью уравнивания. Последующие геологоразведочные работы подтвердили факт существования данного нарушения. При отсутствии нарушений углы напластования изменяются достаточно плавно и в небольших пределах. Данный поисковый признак наличия нарушений основан на усеченном использовании методики И. П. Жингеля [16]. Кроме того, в рассматриваемой ситуации желательно провести повторный анализ каротажных диаграмм на предмет обнаружения зон дробления.
В-четвертых, это нетипичное поведение стволов геологоразведочных скважин. Обычно они искривляются в сторону восстания пластов. Имеющее место обратное явление (рис. 3.31) обусловлено, в подавляющем большинстве случаев некорректностью выполненных построений, связанной с «разворотом» направления падения пластов. Если учет прогнозируемого с помощью уравнивания разрывного нарушения приводит к изменению направления падения пластов и, как следствие, к нормализации поведения ствола скважины, то это становится весомым косвенным аргументом в пользу надежности прогнозных построений.
Для косвенного подтверждения существования разрывных нарушений могут использоваться и традиционные геологические признаки, такие как изменения мощностей междупластья, увеличение кривизны пластов и смещения изогипс.
Необходимость использования рассмотренных выше эмпирических приемов не связана с сущностью метода уравнивания геологоразведочных измерений, а обусловлена реальным качеством отечественной геологоразведочной информации. Эти приемы позволяют достаточно эффективно вести прогнозирование даже в условиях наличия в выборке значительного количества грубых ошибок разведки.
На практике иногда возникают ситуации, которые требуют рассмотрения достоверности изучения поведения пласта в контуре уже нарезанного выемочного контура. Например, в 1996 году одна из кузбасских фирм, ориентированная на подземную отработку пластов, вскрытых углеразрезами, вела поиск инвестиций для приобретения механизированного комплекса для уже нарезанной лавы.
Оценка достоверности горно-геометрических моделей и прогноз нарушенности пласта в таких условиях выполняются на основе результатов стандартных, инструктивно регламентированных геолого-маркшейдерских наблюдений в горных выработках и обладают лишь незначительными специфическими особенностями. Главная из них состоит в том, что в связи с высокой надежностью шахтных наблюдений и возможностью их контрольного повторения полностью отпадает необходимость в сложной и трудоемкой процедуре поиска и отбраковки ошибочных исходных данных. При прогнозировании нарушений допустимо также отказаться от учета градиентов поправок по направлениям, ориентированным вдоль штреков (поскольку они уже были детально изучены в ходе проведения горных выработок). Этот отказ позволяет сформировать более однородную (как по ориентации, так и по расстояниям между замерами) совокупность градиентов, и, как следствие, усиливает рельефность проявления аномальных градиентов.
Поэтому для выполнения прогноза нарушенности в нарезанном выемочном столбе используется специальная программа «PDL». Помимо учета этой особенности, она обладает дополнительными сервисными элементами, что обеспечивает:
- автоматическое определение элементов залегания пласта в точках измерений по их отметкам и углам падения, измеренным в плоскости груди подготовительного забоя;
- производство прогноза с использованием только пространственных координат точек наблюдений;
- определение расстояния между штреками вдоль кровли пласта.
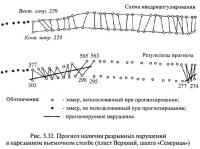
Практическое применение метода уравнивания для прогноза нарушений на шахтах Кемеровского, Ленинского и Беловского геолого-промышленных районов указывает на его высокую точность (подтверждаемость прогнозов составляет 75—90 % для нарушений с амплитудами более 0,5 м). В ходе исследовательских работ установлено, что геологические службы многих предприятий, вопреки действующим инструктивным требованиям, не обеспечивают создание сети геологических наблюдений необходимой плотности и конфигурации и даже не производят измерения элементов залегания пласта. На рис. 3.32 приведены результаты прогнозирования нарушений по одной из лав со 100%-м подтверждением результатов прогноза.
Пример любопытен тем, что проходка конвейерного штрека была прекращена из-за неожиданной встречи разрывного нарушения в точке № 303. Между тем это нарушение надежно прогнозируется методом уравнивания задолго до его встречи (рис. 3.33).
Таким образом, применение уравнивания в процессе проведения нарезных работ, требующее проведения только регламентных измерений, позволяет снизить объем бросовых горных выработок.
Следует подчеркнуть, что использование горно-геометрических методов прогнозирования нарушенности не исключает последующего применения подземного разведочного бурения и геофизических исследований, но позволяет применять их более целенаправленно и эффективно.