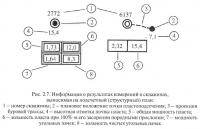
Для пологих (угол падения до 18°), наклонных (19—35°) и части крутонаклонных (36—55°) пластов подсчетные планы выполняются в проекции на горизонтальную, а для крутых (56—90°) и отдельных крутонаклонных пластов — на вертикальную плоскость. На подсчетных планах показываются (рис. 2.8): координатная сетка (в виде квадратов размером 10х10 см), изогипсы пласта (сплошными линиями с цифровым указанием их отметки, обычно предваряемым сокращением «гор.»), оси складок (штрих-пунктирными линиями), устья скважин (двойными окружностями), точки пластоподсечений (точки пересечения стволов скважин с почвой пласта — кружки черного цвета) и другие графико-числовые характеристики, не используемые при расчетах ламбда-критериев.
Для вертикальных скважин точка пластоподсечения совпадает в плане с устьем скважины (скважина 2772 на рис. 2.7), а для наклонных скважин — не совпадает (скважина 6137 на рис. 2.7). В последнем случае точка пластопересечения соединяется с устьем пунктирной линией (теоретически эта линия должна отображать проекцию оси скважины, однако фактически она, как правило, имеет просто характер условного 31 тка). Рядом с каждой точкой пластоподсечения выписываются номер скважины, отметка пластоподсечения (т. е. почвы пласта) в Балтийской системе высот, общая нормальная мощность пласта и зольность пласта при 100%-м засорении породными прослоями, нормальная мощность чистых угольных пачек и их зольность (рис. 2.7). В некоторых случаях значения зольности на подсчетный план не выносятся. Если пласт простого строения (без прослоев), то он имеет, естественно, только одно значение зольности и нормальной мощности (скважина 6137 на рис. 2.7). Важной информацией, помещаемой на плане подсчета запасов, является отметка об использовании данных о мощности и зольности при подсчете запасов. Если результаты измерений использованы при подсчете запасов, то их значения обводятся двойной прямоугольной рамкой (скважина 2772 на рис. 2.7), в противном случае используется одинарная рамка (скважина 6137 на рис. 2.7). В отдельных случаях не принятые в подсчет запасов данные не обрамляются вообще, а принятые в подсчет обводятся одинарной рамкой.
Полное исключение результатов измерений мощности из подсчета запасов, то есть неучет их при выводе средних мощностей по подсчетным блокам, может иметь две причины. Первая состоит в том, что исключаемый замер, по мнению авторов подсчета запасов, вполне надежен, но пласт имеет данную мощность или зольность на весьма ограниченном участке. Принадлежность замера к данному типу далеко не всегда очевидна, исключение составляют, пожалуй, лишь замеры, попавшие в зону действия разрывных нарушений, аномальные значения которых связаны со «сдвоением» пласта из-за перекрытия, его под-воротом, обрезом и так далее. Вторая причина состоит в том, что сам результат измерения подвергается сомнению как произведенный с грубыми ошибками.
Приведенные на рис. 2.7 обозначения несколько различаются для различных бассейнов и даже месторождений, особенно в старой документации. На рисунке приведены условные знаки, характерные для Кузбасса.
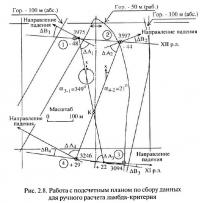
Расчет ламбда-критерия начинается с выделения контура оценочного четырехугольника сети замеров (скважины 3975 — 3597 — 3094 — 3246 на рис. 2.8). После этого прочерчиваются его диагонали (пунктирные линии на рис. 2.8), попарно соединяющие пластоподсечения, и определяется положение точки их пересечения К. Подсечениям присваиваются условные номера от 1 до 4 (цифры в окружностях на рис. 2.8). Затем производятся измерения длин диагоналей 1-3 (между под-сечениями 3975 и 3094 — R = 502 м) и 2-4 (между подсечениями 3597 и 3246 — R' = 497 м), а также расстояний от начальных скважин обеих диагоналей с условными номерами 1 (3975) и 2 (3597) до точки К — L = 303 м и L' = 305 м.
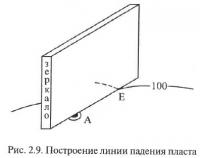
После этого устанавливаются направления падения пластов в точках производства замеров. Проведение этих направлений осуществляется на подсчетном плане, гипсометрия которого отстроена при рациональном сечении изогипс (методика проверки рациональности сечения будет рассмотрена ниже), путем проведения из точки замера перпендикуляра к ближайшей изогипсе. Его построение может производиться на глаз или с помощью зеркала (рис. 2.9). При этом зеркало вертикально устанавливается на центр рассматриваемого замера А и производится его вращение вокруг этой точки до тех пор, пока реальное и отраженное изображение изогипсы в точке Е не сольются в единую плавную кривую, не имеющую в точке Е излома. Это положение грани зеркала соответствует направлению линии падения, которая и прочерчивается, используя зеркало как линейку.
После завершения построений линий падения, для каждого подселения измеряются острые углы ΔВj между направлениями падения и линиями разрезов по разведочным линиям. Для условий рис. 2.8 они равны: ΔВ1 = 25°; ΔВ2 = 24°; ΔВ3 = 4°; ΔВ4 = 21°. Значения углов ΔBj необходимы для определения «истинных» углов падения пласта по углам падения, измеряемым по геологическим разрезам разведочных линий. Измеряются также и острые углы ΔАj между направлениями диагоналей четырехугольного блока и направлениями падения (по результатам измерений эти углы равны: ΔА1 = 51°; ΔА2 = 47°; ΔА3 = 72°; ΔА4 = 82°).
Используя правило, иллюстрированное рис. 2.4, устанавливаются знаки функций T(δj). Для T(δ1), T(δ2) и T(δ4) это «+» (направление диагонали, т. е. направление от замера с меньшим условным номером к замеру с большим условным номером, и направление падения пласта в точке измерений не согласны), а для T(δ3) — «-» (направления диагонали и падения согласны).
После этого обращаются к геологическим разрезам по разведочным линиям и измеряют по ним углы падения пласта δлj в точках пластоподсечений (как углы между касательными к пласту и горизонтальными линиями или, при применении зеркала, как углы между перпендикулярами к пласту и вертикальными линиями). В результате измерений углы δлj составили: δл1 = 21°; δл2 = 25°; δл3 = 5°; δл4 = 12°.
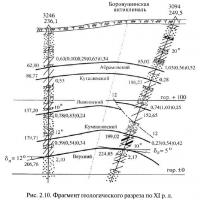
На геологическом разрезе, рядом со структурной колонкой по скважине, напротив точек измерений, приводятся значения измеренных углов напластования пород (например, угол 10° в кровле пласта Верхнего по скважине 3094 на рис. 2.10), т. е. углов наклона плоскостей контактов пород относительно оси керна.
Следует помнить, что эти углы далеко не всегда равны углам падения угольных пластов и, кроме того, не всегда известна пространственная ориентировка линий падения слоев пород по керну (т. е. данный угол может иметь в плоскости заданного разреза совершенно иное значение).
Зная углы ΔВj и δлj по формуле:
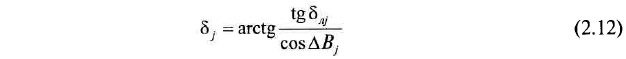
рассчитываются «истинные» углы падения пласта в точках замера (т. е. углы в направлении линий падения пласта ). Для условий рис. 2.8 они равны:

Помимо скважин, входящих в состав разведочных линий, существуют и отдельно расположенные скважины (рис. 2.11), определение угла падения пласта в которых, в силу отсутствия отстроенного геологического разреза, осуществить вышеописанным способом невозможно.
В данной ситуации поступают следующим образом (рис. 2.12). Через точку пластоподсечения (точку S на рисунке) проводится перпендикулярно ближайшей изогипсе линия падения пласта MF, по которой строится совмещенный с планом разрез. Линия MF проводится таким образом, чтобы она пересекала две-четыре изогипсы. Для построения разреза линия MF принимается за горизонт одной из пересекаемых ею изогипс (горизонт ± 0 м на рисунке) и на ней помечаются точки ее пересечения с изогипсами плана (точки А, В, С и D). Для всех i-x точек определяется разность ΔZi их высотных отметок (соответствующих отметкам формирующих их изогипс) и отметки условного горизонта линии MF. Аналогичная разность рассчитывается и для самого пластоподсечения, положение которого обозначено на линии МТ точкой S.
Для условий рис. 2.12: ΔZA = 300 м; ΔZB = 200 м; ΔZC = 100 м; ΔZD = 0 м и ΔZS = 49 м. Затем величины ΔZi откладываются в масштабе плана из соответствующих точек перпендикулярно МТ — в результате на совмещенном разрезе отмечаются точки A', В', С', D' и S', через которые проводится главная кривая, описывающая положение почвы пласта в разрезе по линии падения. На заключительном этапе работы через точку У проводится касательная к кривой А'— В'— С'— S’—D' линия КТ. Угол между КТ и М Т равен углу падения пласта δ в точке пластоподсечения S.
Отметим, что компьютерные алгоритмы процесса построения сонме щенных разрезов рассмотрены в главе 5.
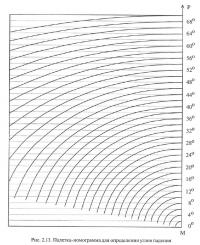
Для упрощения процесса определения углов 8 по формуле 2.12 целесообразно использовать палетку-номограмму, изготавливаемую на прозрачной основе (рис. 2.13).
Для пересчета угла падения пласта δлj измеренного на разрезе по разведочной линии, в его значение по направлению линии падения, палетка-номограмма накладывается на подсчетный план так, чтобы начало координат (точка М) совпадало с точкой замера, а ось МР — с направлением линии падения пласта (рис. 2.14). По оцифрованной шкале углов (расположенной вдоль оси МР) отыскивается точка А, положение которой соответствует значению угла δлj по разведочной линии (24° в примере на рис. 2.14). Из А восстанавливается перпендикуляр к МР до пересечения с линией геологического разреза в точке К.
Путем проектирования положение точки К на шкалу углов параллельно криволинейным шкалам номограммы определяется положение точки В (на рис. 2.14 линия переноса показана пунктирной линией). Отсчет по шкале углов в точке В соответствует значению «истинного» угла падения δj.
Следует особо подчеркнуть, что описанная методика определения значения угла падения пласта в точке пластоподсечения должна применяться даже в случаях, когда в скважинах произведены инструментальные измерения углов падения (с помощью ориентированного керна, наклонометрии, теле- и фотосъемки скважин). Это связано с тем, что в процессе оценки достоверности оценивается неоднозначность модели гипсометрии, и поэтому используемые при расчетах значения углов падения должны обязательно соответствовать этой модели (даже в случае, когда известны действительные значения данных углов).
По завершении работы с углами с подсчетного плана выписываются значения высотных отметок пластоподсечений Zj. Для условий рассматриваемого примера они равны (рис. 2.8):
Однако, к сожалению, подсчетные планы содержат значительное число цифровых ошибок и описок. Поэтому необходимо производить контроль указанных значений высотных отметок.
Контроль выполняется поэтапно. На первом этапе анализируется соответствие указанных отметок подсечений и показанных на плане изогипс почвы пласта (горизонтов) или осей складок.
Таким способом выявляются наиболее грубые ошибки. Например, в случае, когда между изображенными горизонтами «-100 м» и «-200 м» неожиданно появляется пластоподсечение с отметкой +145 м. Применительно к рис. 2.8 такой визуальный контроль приводит к возникновению сомнений относительно правильности отметок по пластоподсечениям скважин 3246 и 3094.
Первое из них расположено выше, чем второе, несмотря на то, что оно значительно дальше удалено от оси складки (наиболее «высокого» места пласта в сечении по разведочной линии, пройденной вкрест простиранию). На втором этапе контроль отметок производится с помощью геологических разрезов. При его выполнении высотные отметки пластоподсечений определяются графически путем измерения расстояния ΔZ от линии горизонта до почвы пласта в точке подсечения. Так, для рассматриваемого примера (рис. 2.15) ΔZ=38 м. Поскольку измерения производились от горизонта «± 0 м», то ожидаемая отметка пластоподсечения по скважине 3094 составляет +38 м, а не +22 м, как указано на подсчетном плане. Кроме того, так как на геологическом разрезе указаны высотные отметки устьев скважин и глубины пластоподсечений, то возможна и арифметическая проверка отметок последних. Например, отметка устья вертикальной скважины 3246 составляет 236,1 м, а глубина подсечения пласта Верхнего 206,76 м. Тогда отметка подсечения составляет: 236,1 м — 206,8 м = 29,3 м, т. е. соответствует приведенному на подсчетном плане. Аналогичные отметки и глубины по наклонным скважинам использовать несколько сложнее. Ориентировочное значение отметки подсечения может быть оценено по формуле:
где Zy — высотная отметка устья скважины;
Н — глубина пластоподсечения;
Θ — средний зенитный угол ствола скважины (угол между осью ствола скважины и вертикалью).
Для рассматриваемого примера по скважине 3094:
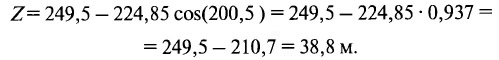
Таким образом, для четырехугольника сети скважин, показанного на рис. 2.8, отметки под сечений равны:
При проведении контрольных работ необходимо иметь в виду, что любые приведенные на чертежах цифры могут быть указаны с описками, тогда как в положении пласта на разрезах и изогипс на планах «опи-ски» совершить в принципе невозможно.
При наличии по участку наклонных и искривленных скважин значительной глубины целесообразно осуществить повторную обработку результатов их инклинометрической съемки (например, с помощью специальной программы [50] для ЭВМ). Это вызвано тем, что фактически такая обработка часто ведется упрощенным графическим способом, приводящим к дополнительным, легко избегаемым погрешностям в плановом положении пластоподсечений. Эти погрешности достигают в среднем 30—50 м для скважин глубиной порядка 500—600 м (т. е. составляют 5—10 % от глубины). Хотя повторные расчеты и необязательны с позиции оценки достоверности геометрической модели (т. к. упомянутые дополнительные погрешности автоматически приводят к снижению уровня однозначности модели), они все же полезны, поскольку позволяют не только увеличить точность данных, но и повысить качество последующих прогнозов дизъюнктивной нарушенности пласта. Кроме того, их результаты позволяют дать общую неформальную оценку инженерной культуры рассматриваемой геологоразведочной организации. Эта оценка может использоваться при принятии решения о привлечении той или иной геологической партии или экспедиции для выполнения разведочных работ.
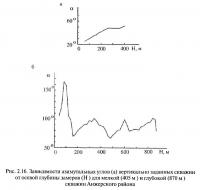
Однако перед производством повторных расчетов необходимо убедиться в том, что инклинометрическая съемка скважины вообще выполнялась. Дело в том, что, согласно действующим инструкциям, точки съемки скважины должны располагаться через 20 м, фактически (в основном для скважин глубиной до 300—400 м) производится один-три реальных замера (в забое, в срединной части и в устье), а значения в остальных якобы существовавших точках измерений «дописываваются» как результат экстраполяции или интерполяции. В отдельных случаях измерения вообще не производятся. Качественно выполненную фальсификацию скважинных инклинометрических измерений выявить весьма трудно, однако практически она выполняется очень грубо. Этим объясняется существенно различный характер зависимости значений азимутальных углов оси скважины от ее осевой глубины для мелких (рис. 2.16, а) и глубоких (рис. 2.16, б) скважин, в которых измерения традиционно производятся тщательно. В первом случае углы почти функционально зависят от глубины, изменяются плавно и в небольших пределах. Во втором случае зависимость имеет статистический характер с последующим переходом к синусоидальным колебаниям, характерным для глубоких скважин, имеющих «винтообразную» пространственную форму.
Авторскими исследованиями, проведенными на материалах инклинометрических съемок геологоразведочных скважин Кузбасса, установлено, что при превышении зенитного угла ствола скважины 3°—5° нерегулярные колебания значений азимутов затухают и приобретают характер закономерных изменений параболического или синусоидального типа. Причины зависимости погрешности значения азимута падения скважины от значения зенитного угла заключаются, по-видимому, во влиянии несовпадения углов падения осей скважины и прибора, степень которого может быть оценена с помощью аналитической формулы:
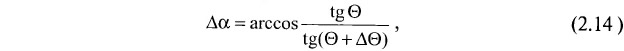
где ΔΘ — рассогласование зенитных углов скважины и прибора;
Δα — погрешность значения азимута, вызванная рассматриваемым рассогласованием.
При ожидаемом значении ΔΘ = 30" погрешность Δα становится значимо (в два раза) меньше технической погрешности измерения азимутальных углов при Θ = 4°. Поэтому, в силу того что в среднем по Кузнецкому бассейну для вертикально забуренных скважин существует тесная корреляционная зависимость между значениями Θ (в градусах) и осевыми глубинами скважин вида
(где Н — осевая глубина замера, сотни метров), закономерные изменения значений азимутальных углов должны наблюдаться с глубин порядка 200 м.
Завершив сбор необходимых исходных данных, производится расчет ламбда-критериев разведанности оценочного блока по формуле 2.6. Расчет целесообразно осуществлять в таблице (см. табл. 2.2).
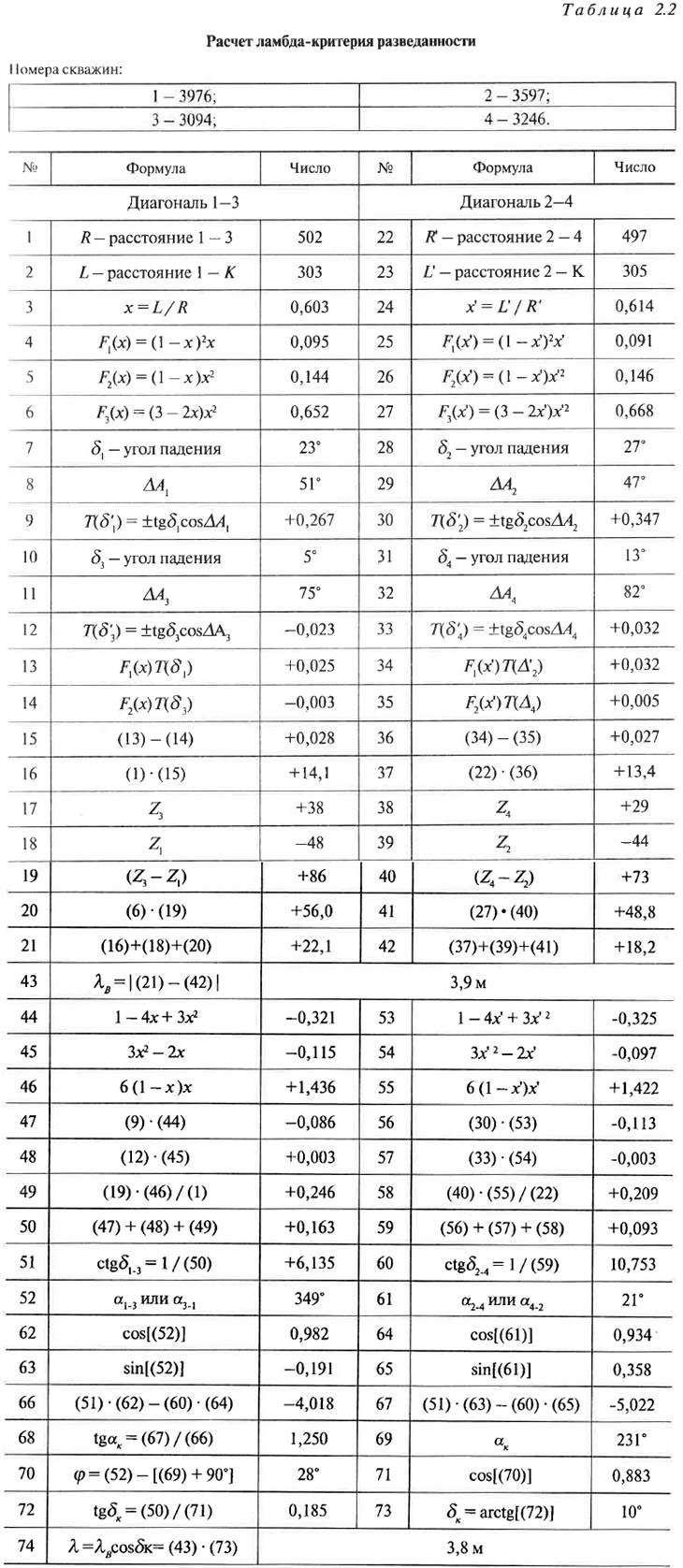
Последовательность вычислительных действий при заполнении таблицы соответствует номерам ячеек.
В графе «Формула» приводятся либо расчетные формулы, либо описывается характер действий с числами, находящимися в указываемых ячейках (например, запись «(6)·(19)» в строке 20 означает, что в нее заносится результат перемножения чисел, находящихся, соответственно, в ячейках с номерами 6 и 19).
Заполнение ячеек 1—43 обеспечивает вычисление значения ламбда-критерия в вертикальном направлении по формуле 2.6, а ячеек 44—74 — перевычисление его в нормальное к пласту направление по формулам 2.8—2.10 и несколько преобразованной формуле 2.11. При заполнении ячеек 52, 61 используются дополнительно снимаемые с подсчетного плана дирекционные углы диагоналей четырехугольника сети замеров. Для этого в произвольной точке каждой диагонали проводится линия, параллельная оси X геодезической системы координат (см. рис. 2.8), от которой в направлении движения часовой стрелки измеряется значение искомого угла. В ячейках 52 и 61, в зависимости от знаков чисел в ячейках 51 и 60 и в соответствии с комментариями к формуле 2.11, приводятся значения дирекционных углов направления 1-3 (или 3-1 — α3-1 или α1-3) и направления 2-4 (или 4-2 — α2-4 или α4-2). В соответствии с этими замечаниями в ячейке 51 указан дирекционный угол направления 3—1 — α3-1 в ячейке 60 — α4-2. При определении величины дирекционного угла αк линии простирания пласта в точке пересечения диагоналей К (ячейка 69) по значению его тангенса, указанного в ячейке 68, пользуются правилами, приведенными в табл. 2.3.

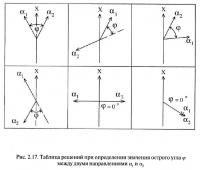
При вычислениях следует обратить внимание на особенность расчета величины острого угла φ между направлением падения пласта по диагонали 1—3 (ячейка 52) и направлением линии падения пласта в точке К (ячейка 70). При расчете в первую очередь определяется направление линии падения αп (указанное в ячейке 70 в виде формулы [(69) + 90°]), путем увеличения угла αк на 90°. В рассматриваемом примере оно равно 321° (231° + 90°). Если полученная величина αп превысила бы 360°, то из результата следовало бы вычесть 360°. Например, при αк = 311°, угол αп составил бы 311° + 90° = 401° или после вычитания 360° — 41°. После расчета величины αп определяется собственно острый угол φ между направлениями αп и направлением, указанным в ячейке 52 (α1-3 или α3-1). При вычислении угла φ не следует забывать о специфике вычитания углов в условиях, когда один из них находится в диапазоне от 0° до 90°, а другой — от 270° до 360° (см. примеры на рис. 2.17). Естественно, что угол ф всегда положителен.
Производство пересчета вертикального значения ламбда-критерия в перпендикулярное к пласту направление имеет смысл осуществлять только при более чем 20-градусном значении угла падения пласта в точке пересечения диагоналей. Поэтому, если имеется твердая уверенность в том, что δк < 20°, ячейки 44—74 табл. 2.2 могут не заполняться.
Ручной вариант расчета ламбда-критериев приведен практически только с целью иллюстрации алгоритма его выполнения. При выполнении реальных расчетов используется компьютерная технология обработки данных. Перечень и порядок подготовки необходимой для ее производства информации несколько отличаются от вышеописанных. Форма таблицы исходных данных, ориентированной на программу «DRU», приведена в табл. 2.4. Порядок заполнения колонок 8—10 таблицы, предназначенных для занесения данных, используемых при производстве оценки достоверности моделирования мощности и зольности пласта, будет рассмотрен несколько позже.
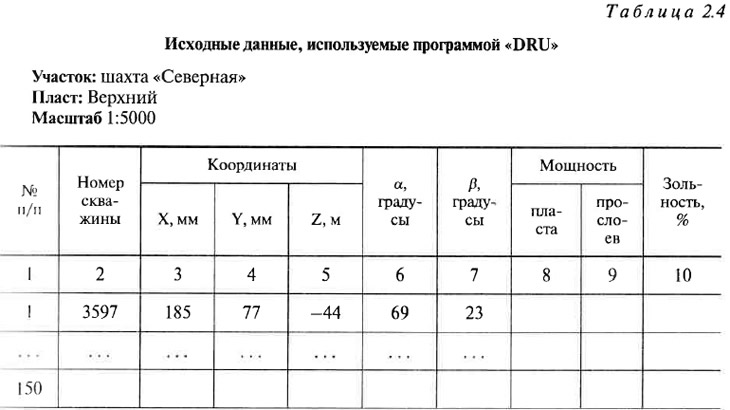
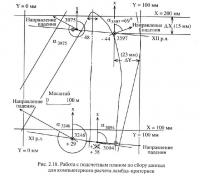
Работа с табл. 2.4 начинается с занесения наименования объекта исследований (строки «Участок» и «Пласт») и указания масштаба подсчетного плана (строка «Масштаб»). После этого производится оцифровка координатной сетки плана (рис. 2.18). Оцифровка производится в миллиметрах (т. е. каждая следующая линия сетки имеет координату на 100 мм больше, чем предыдущая). Выбор начальной точки оцифровки должен обеспечивать положительность значений координат всех пластоподсечений. Кроме того, описанными ранее способами прочерчиваются линии падения пласта, определяются значения дирекционных углов а. этих линий, производится контроль значений высотных отметок подсечений и измеряются величины углов падения пласта δi в них. По завершении подготовки планов к работе приступают собственно к сбору данных.
Для каждого пластоподсечения графически определяются плоские координаты X и Y. При этом измеряются приращения ΔХ и ΔY от ближайших линий координатной сетки до центра точки подсечения. Окончательные значения координат получают путем сложения или вычитания приращений и координат соответствующих линий сетки. Производство измерений именно от ближайших координатных линий осуществляется с целью минимизации погрешностей измерений, связанных с деформацией прозрачной основы графических материалов при светокопировании (поскольку в настоящее время геологическая документация распространяется только в виде светокопий). Например, подсечение 3597 на рис. 2.18 находится на 15 мм ниже координатной линии 200 мм оси X и на 23 мм левее линии 100 мм оси Y. Поэтому координата X подсечения равна в данном случае 185 мм (200 — 15), а координата Y: 77 мм (100 — 23).
Полученные значения координат записываются в колонки 3 и 4 табл. 2.4. В столбце 2 таблицы указываются истинные номера скважин, а в колонки 5—7 заносятся соответственно высотные отметки пластоподсечений Zi (в метрах), дирекционные углы αi направлений линий падения пласта и углы падения δi.
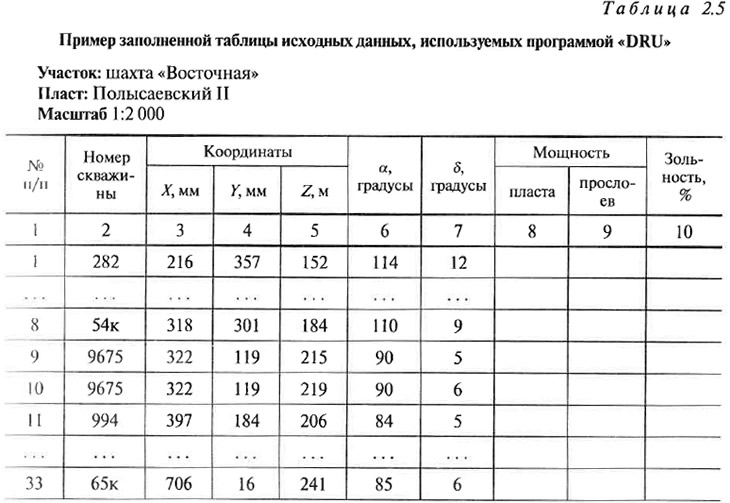
В случае если по скважине имеет место двукратное подсечение пласта (вызванное наличием зоны его перекрытия, возникшей в результате воздействия разрывного нарушения), то при формировании таблицы исходных данных оба подсечения (имеющие, естественно, одинаковый номер) должны располагаться последовательно друг за другом. Сведения о прочих подсечениях могут заноситься в таблицу в абсолютно произвольном порядке. Например, в табл. 2.5 приведен фрагмент исходных данных, в которых по скважине номер 9675 (порядковые номера 9 и 10) пласт, в силу наличия зоны перекрытия, встречается дважды.
Квадриангулирование сети измерений (создание системы выпуклых четырехугольников с вершинами — точками измерений) выполняется при работе с программой в интерактивном режиме. При этом на экране ЭВМ возникает изображение сети измерений (рис. 2.19), на котором с помощью маркера мыши пользователь должен отметить вершины выделяемого четырехугольника.
Выделение производится путем обхода точек замеров — вершин четырехугольника по (или против) направлению движения часовой стрелки. По завершении выбора вершин блока автоматически осуществляется контроль корректности его геометрической формы, по результатам которой он принимается в дальнейшую обработку.
В силу того что реальные разведочные сети, как правило, нерегулярны, иногда при квадриангулировании возникают неоцениваемые области. С наличием таких зон приходится, к сожалению, просто мириться (рис. 2.20). Следует особо отметить, что выделяемые оценочные блоки могут накладываться друг на друга.
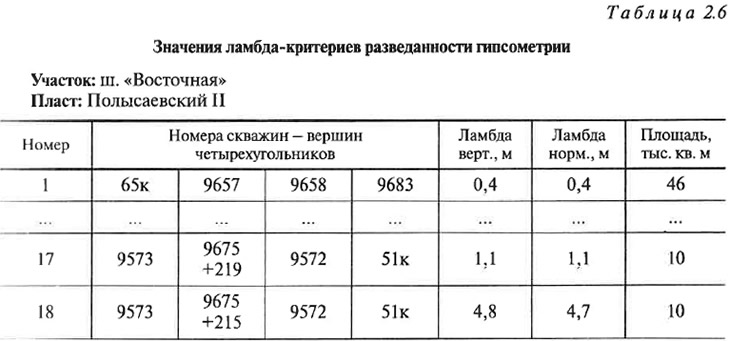
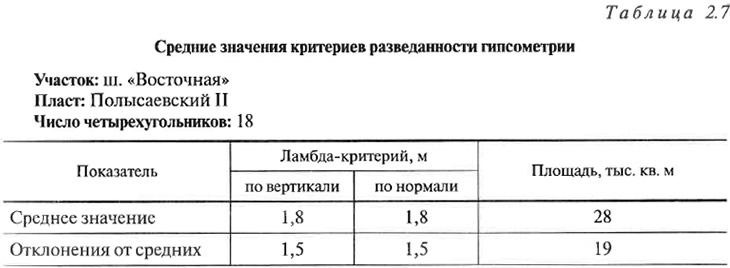
В результате обработки программой «DRU» квадриангулированных данных выдается таблица значений ламбда-критериев (табл. 2.6). В случае если имеет место двукратное пересечение пласта скважиной (если она подсекает зону перекрытия пласта), то под номером входящей в оценочный блок скважины указывается высотная отметка использованного при расчетах пластоподсечения (соответственно «+219 м» в блоке номер 17 и «+215 м» в блоке номер 18 по скважине 9675 в табл. 2.6). Кроме того, приводится и информация о среднем значении критерия в целом по объекту (табл. 2.7), впоследствии используемая при оценке правомерности расчета ламбда-критериев разведанности.
Помимо интерактивного режима, существует пакетный режим квадриангулирования (программа «PRNGEO»). В его основе лежит авторский алгоритм, использующий известные методы а-триангуляции сети наблюдений [20].
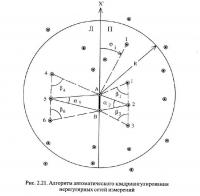
Алгоритм предусматривает, что выделение четырехугольников производится индивидуально для каждого отдельного замера. Рассмотрим его применительно к замеру А на рис. 2.21. Ясно, что другие вершины оценочного блока будут находиться в его окрестностях.
Выделить такие замеры можно по условию их попадания в круг радиуса R, построенный вокруг точки А. С практической точки зрения достаточно принять радиус Я кратным среднему расстоянию между замерами в сети — G.
Оценка значения G может быть выполнена следующим образом. Для каждого i-то замера отыскивается ближайший к нему замер, удаленный от него на расстояние li. Ясно, что в большинстве случаев для условий геологоразведочных данных li будет соответствовать расстоянию между скважинами в разведочной линии. Поэтому среднеарифметическое значение li является достаточно точной оценкой расстояния G. Экспериментально установлено, что вполне приемлемо принимать R равным пятикратному значению G.
В качестве второй вершины оценочного блока принимается ближайший к замеру А замер В.
Для выбора других вершин четырехугольника вводится условная система координат, ось X' которой совпадает с направлением В-А. Для каждого i-го замера, попадающего в круг радиуса R, в осях условной системы координат вычисляется дирекционный угол направления А — I — φi. По результатам расчетов углов φi все замеры разделяются на две группы: расположенные в правой (0° ≤ φi < 180°) и левой (180° ≤ φi < 360°) части круга. Именно в этих частях и должны располагаться выделяемые оценочные блоки.
Третья вершина блока выбирается отдельно для левой и правой групп точек измерений. Принцип выбора основан на методе α-триангуляции и состоит в следующем. Для каждого i-го замера рассматриваемой части круга на базовой стороне A-В строится треугольник ABJ (например, треугольники АВ1, АВ2, АВЗ и т. д. для замеров правой части круга) и определяется величина угла при его вершине J—αj. Анализируя значения таких углов всех сформированных треугольников, находится замер, соответствующий минимальному значению угла а . Этот замер принимается в качестве третьей вершины блока. Для условий рис. 2.21 такими вершинами являются замеры 2 (для правой части) и 5 (для левой части).
Четвертая вершина выбирается аналогично третьей. Для этого по каждой части круга последовательно рассматриваются направления, соединяющие пары ранее выделенных вершин: первая-третья и вторая-третья, которые рассматриваются как базовые стороны (аналогичные A-В). Например, выбор четвертых вершин для группы вершин А, В и 2 (правая часть) производится следующим способом. Рассматриваетси базовая сторона А-2 и определяется ее дирекционный угол в условной системе координат φА-2. После этого, анализируя k-е замеры, расположенные в правой части круга и имеющие дирекционные углы φк меньшие по значению, чем φА-2, находится один из них, угол βк, для которого в треугольниках вида АК1 минимален. Этот замер (номер 1 на рис. 2.21) является искомой четвертой вершиной первого выделяемого четырехугольника A-1-2-В. Затем рассматривается вторая базовая сторона В-2 и определяется ее дирекционный угол φB-2. Анализируя n-е замеры, также расположенные в правой части круга, но имеющие дирекционные углы φN большие, чем φВ-2, отыскивается замер, угол βN для которого в треугольниках вида AN1 минимален. Он (3 на рис. 2.21) используется в качестве четвертой вершины второго выделяемого четырехугольника A-2-3-B. Аналогичным образом в левой части круга формируются оценочные блоки А-В-5-4 и А-В-6-5.
При реализации рассматриваемого алгоритма на ЭВМ значения углов αi (βi), в целях упрощения вычислительных процедур, заменяются на их косинусы, рассчитываемые с использованием известной теоремы косинусов:
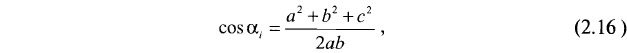
где с — длина базовой стороны треугольника (противолежащей искомому углу, например, стороны A-B при расчете углов αi на рис. 2.21);
a и b — длины прочих сторон треугольника.
Реализация данного подхода приводит лишь к замене используемой при описании процедуры поиска максимального значения угла процедурой поиска минимального значения косинуса.
Полный алгоритм программы «PRNGEO» имеет ряд специфических особенностей, позволяющих решать возникающие при квадриангулировании частные задачи. Например, автоматически анализировать и разрешать ситуацию, когда при квадриангулировании на точку А выяснится, что исходная пара замеров A-В была уже ранее использована при выделении четырехугольников.
Естественно, что каждый выделенный четырехугольник проверяется на приемлемость его геометрической формы и фиксируется программой только в случае, если он не был сформирован ранее, в ходе квадриангулирования на другие точки сети замеров.