Уравнивание нерегулярных цифровых моделей и его практическое использование

Уравнивание нерегулярных цифровых моделей скрытых поверхностей топографического порядка является одним из самых молодых методов обработки геоинформации. Разработка его была начата в 1977 г., а первая открытая публикация появилась в 1979 г. [42]. Полученные теоретические и практические результаты позволяют утверждать, что методы уравнивания складываются в новое самостоятельное направление. Сама идея уравнивания, в принципе, не нова, она применяется в геодезии еще со времен К. Гаусса, имеются хорошо разработанные инструкции, руководства и учебники. Однако в процессе обработки геоинформации попытки уравнивания нерегулярных цифровых моделей, в качестве которых, как правило, выступают сети геологоразведочных измерений (в силу чего метод может квалифицироваться и как метод уравнивания геологоразведочных сетей измерений), до 1977 г. никогда не предпринимались и соответствующие идеи не высказывались.

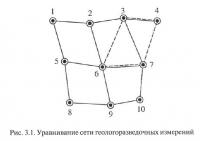
Пусть дана сеть измерений, в каждом из которых определено значение изучаемого признака (рис. 3.1). Квадриангулируем ее, т. е. разделим на систему выпуклых четырехугольных оценочных блоков, которые могут быть как независимыми (например, 1 — 2 — 6 — 5 и 5 — 6 — 9 — 8), так и перекрывать друг друга (2 — 3 — 7 — 6 и 3 — 4 — 7 — 6).

Для каждого оценочного блока в соответствии с формулой 2.1 определим критерий разведанности К_кр (в случае если рассматриваемый признак есть высотная отметка, то им является ламбда-критерий, если мощность пласта и показатели качества угля — то абсолютный дельтакритерий).

Исходя из теоретического равенства критерия нулю, сами значения критериев можно рассматривать в качестве своего рода «невязок», то есть в качестве меры выполнения геометрического, объективно существующего условия. Имея значения критериев (невязок) по всем блокам сети, можно поставить задачу, именуемую задачей уравнивания. Необходимо найти величины (поправки), на которые следовало бы изменить значения измеренных в точках измерений параметров, с тем, чтобы невязки по всем блокам одновременно стали равными нулю. Так как критерии обусловлены погрешностями измерений и интерполяции (а при изучении гипсометрии — влиянием неизвестных тектонических нарушений), то и полученные поправки объективно зависят от этих факторов. Именно эта зависимость и лежит в основе уравнивания как метода анализа.


Особо следует подчеркнуть, что методика использования результатов уравнивания не предполагает производства корректировки результатов выполненных измерений и определений. Поправки рассматриваются лишь в качестве показателя степени влияния погрешности измерения и интерполяции действующих в окрестностях характеризуемых ими точек производства измерений.

Само уравнивание рекомендуется производить методом условий и сводится к следующему. Пусть нами уравнивается признак Р, зная который, по каждому i-му блоку сети по правилу F(P_1i, Р_2i, Р_3i, Р_4i) находится значение необходимого критерия разведанности К_kpi. Тогда можно записать систему, состоящую из n уравнений вида:


где К_ki — значение признака в скважине (замере), входящей в i-й оценочный блок под условным номером к.

Для того чтобы в уравнении 3.1 устранить невязки, необходимо исправить результаты измерений в каждом k_i-м замере на некоторую поправку ε_ki, т. е. превратить их в уравненные значения:


Следовательно, после уравнивания должно быть получено:


Вычтем из каждого из n уравнений вида 3.3 соответствующие уравнения типа 3.1 и получим уравнение:



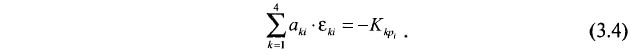
где a_ki — числовой коэффициент.

Если получаемое уравнение 3.4 не является линейным, то 3.3 предварительно разлагается в ряд Тейлора [31], ограничиваясь из-за малости поправок членами разложения, содержащими их только в первой степени. Однако при уравнивании геологоразведочных сетей необходимость такого ослабляющего действия не возникает из-за изначальной линейности уравнения 3.4. Далее система уравнений типа 3.4 решается под условием минимума суммы квадратов поправок.

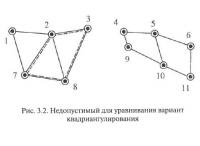
Квадриангулирование сети замеров для уравнивания целесообразно производить несколько иначе, чем для расчета критериев разведанности. Основные различия в подходах, иллюстрируемые рис. 3.2 и 3.3, состоят в том, что при уравнивании:

• необходимо исключать использование блоков или их групп, вообще не имеющих общих точек с другими блоками и их группами (например, на рис. 3.2 группа блоков, использующих скважины 1, 2, 3, 7, 8, «оторваны» от блоков, формируемых скважинами 4, 5, 6, 9, 10, 11, т. е. в приведенном варианте квадриангулирования отсутствует некорректный по форме связующих блок 3-4-9-8);
• желательно обеспечить минимальное число перекрывающих друг друга блоков (если на рис. 3.3, а перекрывают друг друга сразу четыре блока: 1-2-8-7, 2-3-8-7, 3-4-8-7 и 3-9-8-7, то на рис. 3.3, б только два: 1-2-8-7 и 2-3-8-7);
• целесообразно, чтобы все выделяемые четырехугольники сети замеров имели общие стороны (на рис. 3.3,а сторона 4-9 блока 4-5-10-9 не используется в других четырехугольниках, тогда как на рис. 3.3,6 она является стороной блока 3-4-9-8);
• в целях выполнения вышеперечисленных рекомендаций допустимо использование блоков неоптимальной формы (например, блок 3-4-9-8 на рис. 3.3,6 некорректен с точки зрения расчета критериев разведанности).

Рис. 3.1. Уравнивание сети геологоразведочных измерений

Рис. 3.2. Недопустимый для уравнивания вариант квадриангулирования

Допустимость последнего условия объясняется тем, что при уравнивании критерии разведанности выполняют функции объективно существующего геометрического условия, а при оценке достоверности — показателя ожидаемой степени неоднозначности геометрической модели.