Влияние погрешностей измерений исходных данных на значения дельта-критериев разведанности

Значения дельта-критериев разведанности обусловлены действием двух основных факторов:

• техническими погрешностями измерений и определений данных по пластоподсечениям;
• погрешностями применяемого метода интерполирования (метода построения геометрической модели).

Выявление уровня значений дельта-критериев разведанности, связанного только с влиянием технических погрешностей определений параметров, имеет важное значение. Если в ходе исследований объекта будет установлено, что значения критериев целиком обусловлены погрешностями измерений, то, несмотря на их значения, следует сделать вывод об его полной разведанности, т. е. об исчерпании информационных возможностей буровой разведки, проводимой с помощью определенного оборудования и методик.

Предрасчет значения дельта-критерия, обусловленного только уровнем технических погрешностей исходных данных (Δ_р), можно осуществить на основе известных методов теории погрешности измерений. Учитывая, что диагонали оценочных блоков пересекаются где-то в районе их середины и предполагая равенство значений погрешностей однотипных характеристик по входящим в блок скважинам, можно записать:


где Δ₁ и Δ₂ — ожидаемые погрешности определения значения признака в точке пересечения диагоналей четырехугольника, соответственно, по первой и второй его диагонали.

Расчет значения среднеквадратической погрешности Δ_j осуществляется по формуле:


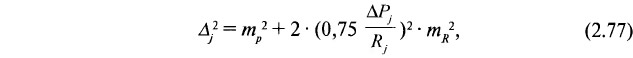
где m_р — среднеквадратическая погрешность непосредственного определения значения изучаемого признака Р (мощности пласта, зольности, теплоты сгорания и т. д.);


m_R — среднеквадратическая погрешность определения длины диагонали;
R_j — длина j-й диагонали;
ΔР_j — разность значений признака между замерами, формирующими j-ю диагональ.

Значение погрешности m_R определяется в соответствии с рекомендациями, изложенными в параграфе 2.10.

Погрешности измерения значений признаков могут быть установлены по материалам ведения горных работ, и даже для мощности пласта, только по материалам разведки.

Как известно, все измерения производятся с погрешностями. Не составляет исключения и процесс измерения мощностей пластов и показателей качества углей в скважинах и горных выработках. Однако измерения, выполняемые на стадии горно-эксплуатационных работ, с точки зрения геометризации могут считаться безошибочными. Это следует из того, что погрешности малы (например, по мнению И. Н. Ушакова, погрешность измерения мощности составляет не более 2—3 %) и являются малозначимыми для горного производства.

Иное дело погрешности скважинных измерений, которые могут достигать значительных величин (например, значения мощностей пластов, измеренные в скважинах, могут содержать погрешности, достигающие 20—40 см).

Методика оценки точности скважинных измерений в условиях уже действующих предприятий вполне очевидна: сравнить данные геологоразведки с данными горных работ, принимая последние за безошибочные. Однако здесь присутствует одно «но». В шахтных условиях практически нет возможности осуществить измерения признаков именно в тех точках, где скважина встретила пласт, хотя к этому и следует стремиться. Кроме того, точки таких замеров находятся, как правило, в зоне опорного давления. Поэтому реально сопоставляются не совпадающие в пространстве замеры в скважинах и в шахте, удаленные друг от друга на расстояние l. Вполне понятно, что такие разнесенные в пространстве сопоставления не вполне достоверны, так как разности «данные геологоразведки — данные горных работ» содержат в себе не только составляющие, обусловленные погрешностями измерений, но и составляющие, связанные с природным, реально существующим, изменением значений признака в пространстве недр. Отсюда сразу встает задача об учете величины l и установлении ее предельного значения.


В соответствии с хорошо подтвердившимися на практике представлениями изменение значений признаков имеет сложный волнообразный характер, осложняющий закономерное прямолинейное изменение признака (рис. 2.71). Исходя из этого, следует, по крайней мере, два вывода. Во-первых, существует некоторое расстояние l₂, при превышении которого сопоставления осуществлять неправомерно, и, во-вторых, в интервале удалений от 0 до l₂ отсутствует прямая зависимость между степенью надежности сопоставлений и расстояниями. Например, сопоставление результата измерения в скважине с замером, удаленным от нее на l₁, даст менее точные результаты, чем сопоставление с замером, удаленным на расстояние l₂, несмотря на то, что l₁ значительно меньше, чем l₂ (рис. 2.71).

При решении задачи оценки точности измерений следует иметь в виду следующее обстоятельство. Поскольку истинный характер изменения признака неизвестен (сведения о длине «волн» отсутствуют), то при любой методике обработки сопоставлений в оцененной величине погрешности измерений будет присутствовать составляющая, связанная с изменчивостью признака, и весь вопрос состоит в том, насколько опасна эта составляющая, насколько она может деформировать генерируемые выводы. Характер влияния случайной составляющей изменения признака на точность модели совершенно аналогичен влиянию на нее погрешности измерений. Поэтому с точки зрения геометризации разделять эти два элемента изменчивости вовсе нет необходимости. Влияние же закономерной составляющей изменчивости, связанной с расстоянием между точками сопоставления, должно быть исключено в максимальной степени.


Исходя из вышесказанного, в основу методики сопоставлений может быть положено следующее представление [27; 28]:


где R_p — свободная от систематической составляющей разность между значениями признака (мощности, зольности и т. д.) по данным горных и геологоразведочных работ;
l — расстояние между точкой замера признака в горной выработке и скважиной;
m_р — среднеквадратическая погрешность измерения значения признака в скважине;
а — коэффициент влияния закономерной составляющей изменчивости на результаты сопоставлений.

Таким образом, различие между данными горных и геологоразведочных работ слагается из погрешности измерений и зависящий от расстояния между точками замера закономерной составляющей изменчивости.

Имея ряд сопоставлений (не менее 20), можно записать систему уравнений вида 2.78, решить ее по методу наименьших квадратов и найти параметры а и m_р.

Нахождение свободных от систематических составляющих разностей осуществляется по формуле


где Р_сi — значение измеренного в скважине признака в i-м сопоставлении;
P_гj — значение измеренного в горной выработке признака в i-м сопоставлении;
с — систематическая составляющая.

Составляющая с рассчитывается для всего массива сопоставлений следующим образом:



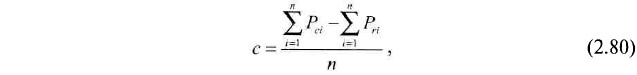
где n — число сопоставлений.

Определение и учет погрешности с необходимо производить лишь в случае, когда она имеет статистически значимый характер. Оценку ее значимости достаточно просто можно установить с помощью несложного метода [43].

Его сущность состоит в следующем.

Пусть имеется совокупность сопоставлений значений признаков по данным горных (P_гj) и разведочных работ (Р_сi) — таблица 2.22.


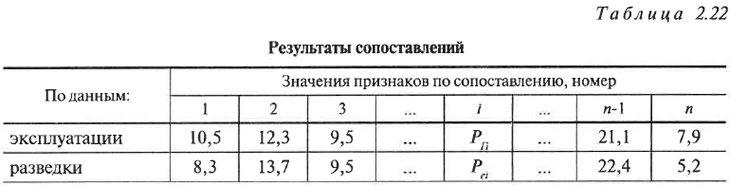
Если рассматриваемые источники данных имеют систематические расхождения в результатах измерений, то должна наблюдаться определенная закономерность в соотношении их значений. Например, первый метод определения (данные эксплуатации), может иметь в основном более высокие значения признака и т. д. Причем это явление должно наблюдаться вне зависимости от того, какой характер имеют систематические погрешности: постоянный или связанный со значением измеряемого признака. Для вскрытия и анализа значимости этих расхождений непосредственные измерения переводятся в ряд натуральных чисел путем их ранжирования. Для этого максимальному значению признака в сопоставлении присваивается ранг b_ij = 1, а минимальному — b_ij = 2. Если значения признаков равны, то обоим присваивается одинаковый ранг 1,5. В соответствии с описанными правилами, после проведения ранжирования данных, табл. 2.22 примет вид табл. 2.23.


Ясно, что наличие систематических погрешностей должно приводить к появлению закономерностей в распределении ранжированных значений измерений по сопоставлениям, т. е. к статистически значимой «похожести», находящихся в колонках последовательностей рангов. Данное обстоятельство легко оценивается с помощью коэффициента конкордации W. Для расчета W находятся суммы записанных в строках таблицы чисел


и параметр

где n — число выполненных сопоставлений.

Собственно коэффициент конкордации W рассчитывается по формуле:


Значение коэффициента изменяется от 0 (полное отсутствие какой-либо закономерности в размещении рангов, а следовательно, и систематической составляющей) до 1 (идеальное совпадение последовательности рангов и, следовательно, чрезвычайно ярко выраженное наличие систематической составляющей). Расчет систематической погрешности по формуле 2.79 и ее последующий учет целесообразно проводить только при W≥0,6.

Решение системы уравнений вида 2.79 по методу наименьших квадратов приводит к расчетным формулам 2.84 и 2.85.

Знак при а² может быть как положительным, так и отрицательным и зависит от положения точек замера относительно «гребней» и «впадин» реального закона изменения признака. Знак при m_p², напротив, всегда должен быть положителен. Отрицательное значение m_p² свидетельствует о наличии в массиве сопоставлений разностей, обусловленных не случайными, а грубыми ошибками и указывает на необходимость производства отбраковки данных. При расчете сумм, используемых в формулах 2.84 и 2.85, чисто из вычислительных соображений рекомендуется измерять l в сотнях метров.


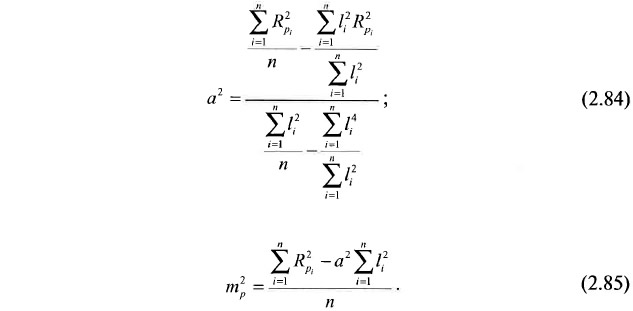
Поскольку довольно рискованно производить сопоставления на расстояниях, при которых существенно влияние закономерных составляющих, результаты сопоставлений можно считать достоверными лишь в случае, если:


где l_ср — среднеарифметическое расстояние между замерами и скважинами.

Оценку точности целесообразно проводить в три этапа. Первый из них состоит в расчете а и m_р по заданному массиву сопоставлений. На втором этапе осуществляется выявление абсолютно ненадежных сопоставлений на основе построения графика зависимости квадратов фактических разностей значений показателя (R_pi²) от квадратов расстояний сопоставлений (l_i²) — рис. 2.72. На этот же график наносится и теоретическая прямая R_p² = m_р² + а² · l². Корреляционное облако может иметь одну из форм. Наиболее часто форма облака соответствует рисунку 2.72, а и не имеет каких-либо закономерностей.

Для выявления ненадежных сопоставлений находится среднеквадратическое отклонение квадратов теоретических и фактических значений по формуле


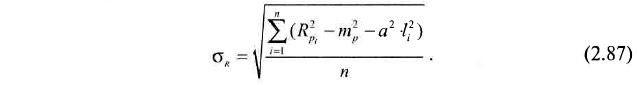
Ненадежным в этом случае полагается сопоставление, для которого модуль разности R_p² — m_p² + а² · l² превышает 1,5σ_R.

Иногда, когда направления линий, соединяющих сопоставляемые замеры в горных выработках и в скважинах, близки между собой, корреляционное облако зависимости имеет волнообразную форму (рис. 2.72, б). «Гребни» и «впадины» волн облака соответствуют «гребням» и «впадинам» волн, собственно изменения. Сопоставления, попавшие в них, нельзя считать надежными. В этом случае вдоль границ корреляционного облака проводятся линии (пунктиры — на рис. 2,72, б), как бы отсекающие «гребни» и «волны». Все сопоставления, попавшие выше и ниже этой пары линий, признаются ненадежными.

Третьим этапом обработки является окончательный расчет параметров а и m_р только по надежным замерам. Полученное на этом этапе значение систематической погрешности целиком относится к скважинным измерениям. Однако ее не следует интерпретировать как реально существующую погрешность, если она меньше, чем половина погрешности m_р. При оценке точности измерений мощностей не следует забывать, что величина с может быть вызвана неучтенным действием опорного давления.

При выполнении сопоставлений необходимо обеспечить постоянство методики выполнения скважинных измерений, что достигается в ходе формирования массивов исходных данных. Наиболее просто это достигается путем включения в массив сопоставлений скважин только одной стадии разведки. Выделить их на подсчетном плане или на плане горных работ очень просто по номерам скважин, первые цифры которых, как правило, постоянны для каждой стадии. Недопустимо использовать при сопоставлениях результаты измерений, не принятые в подсчет запасов. При сопоставлениях мощности следует иметь также в виду, что в пределах массива сопоставлений мощность по скважине должна быть принята по одним и тем же данным (например, по каротажу). Дело в том, что измерения, выполненные по каротажу, не содержат, а буровые измерения содержат систематические погрешности. Таким образом, в ходе оценки точности могут возникнуть несколько массивов сопоставлений, обрабатываемых независимо друг от друга.

При выборе пар сопоставлений вполне допустимо производить сравнение данных по одной скважине с несколькими замерами. Однако число таких сопоставлений должно быть примерно постоянным для каждой скважины, так как в противном случае произойдет смещение оценки в сторону конкретной погрешности, имеющей место в скважине с большим числом сопоставлений. В этом случае результаты оценки точности не будут представительными, а следовательно, и надежными.

В качестве поясняющего примера рассмотрим процесс сопоставления данных горных и разведочных работ по зольности одного из пластов разреза «Междуреченский» (рис. 2.73). В целях сокращения объема расчетов пример сознательно выполнен по некорректно малому числу сопоставлений.

При выполнении сбора исходных данных на плане горных работ намечаются пары сопоставлений «скважина — замер» (которые соединены на рис. 2.73 прямыми линиями). Измеренные длины этих линий l и значения зольности заносятся в таблицу исходных данных (табл. 2.24).


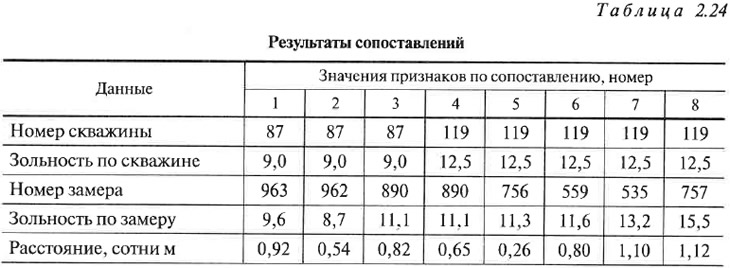
Для сопоставлений выбираются те замеры по горным работам, которые находятся как можно ближе к скважинам, но не «экранируют» друг друга.

Поэтому, например, в сопоставлениях не используется замер 901, «экранируемый» относительно скважины 119 замером 756 (несмотря на то, что он более близок к данной скважине, чем используемые замеры 559, 535 и 811).

В случае, если по участку отстроены изолинии значений признака по данным горно-эксплуатационных работ, в качестве наиболее предпочтительных направлений сопоставлений желательно принимать направления, совпадающие с направлением изолиний (т. к. вдоль них природная изменчивость признака минимальна).

На первом этапе оценки точности оценивается значимость систематической составляющей, для чего создается таблица рангов результатов измерений (табл. 2.25).


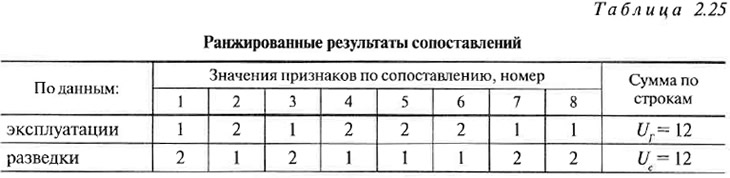
По результатам расчетов сумм U_r и U_c по формуле 2.82 получаем: S = (12 — 1,5 · 8)² + (12 — 1,5 · 8)² = 0 и по формуле 2.83 W=0. На основании этого можно сделать вывод о полном отсутствии систематической составляющей в результатах сопоставлений. Поэтому не возникает необходимости в использовании формул 2.79 и 2.80 для установления и учета систематических погрешностей.

Затем производится предварительный расчет значений погрешностей а и m_р. Для определения необходимых для этого сумм значений признаков формируется специальная таблица 2.26.


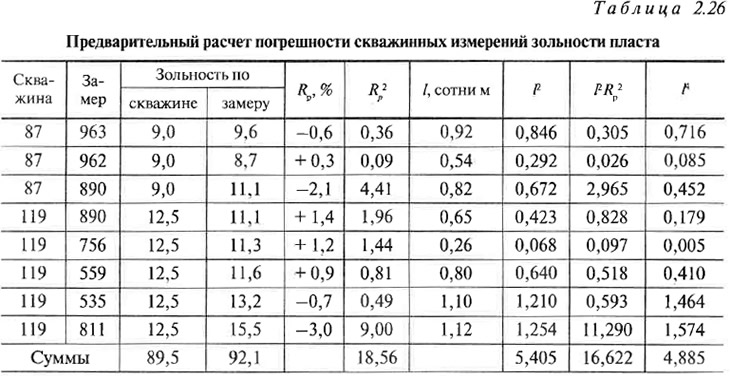
В соответствии с формулами 2.84 и 2.85 погрешности равны:


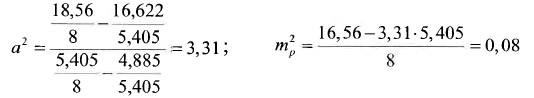
и а = 1,82; m_p = 0,3 %

Для установления вида корреляционного облака и выделения и исключения очень грубых сопоставлений строится график зависимости значений R_p² от l² (рис. 2.74). Рассчитанное по формуле 2.87 среднеквадратическое отклонение σ_R равно 2,25. На рисунке, параллельно аппроксимирующей прямой, на удалении по вертикали от нее ±1,5 проводятся две линии (пунктиры на рис. 2.74), отсекающие точки, соответствующие грубым сопоставлениям. Как видно из рисунка, к ним можно отнести только сопоставление № 8 (между скважиной 119 и замером 811). Данное сопоставление исключается из исходной таблицы 2.26, и все вычисления повторяются вновь (табл. 2.27).


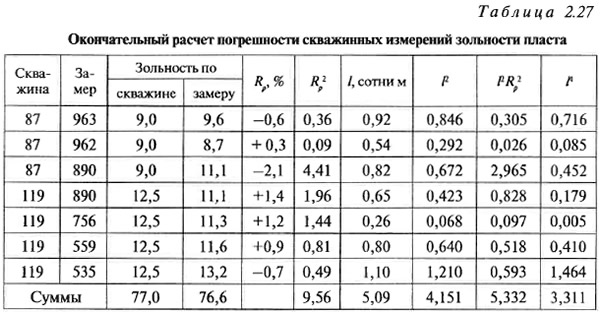
После вычислений по формулам 2.83 и 2.84 получаем: а² = —0,395; m_p² = 1,13, т. е. а = 0,628; m_р = 1,06 %.

Результаты расчетов проверяются на надежность по условию формулы 2.85: 1,06≥3·0,395·0,79 или после вычислений: 1,06≥0,94. Поскольку оно выполняется, то дальнейшая отбраковка данных не требуется (если бы оно не выполнялось, то следовало бы продолжить отбраковку данных). Таким образом, ожидаемая техническая погрешность определения зольности пласта III в условиях углеразреза «Междуреченский» составляет ±1,1 %. Еще раз напомним, что рассмотренный пример выполнен по чрезмерно усеченному массиву сопоставлений (по полному массиву данных, состоящему из 72 сопоставлений, была получена погрешность определения зольности ±1,3 %).

Существует еще один достаточно простой способ оценки точности скважинных измерений. Он состоит в том, что предварительно, по материалам горных работ, отстраиваются изолинии фактического поведения признака на участке сопоставления. Используя эту модель (которая очень близка к реальности), находят значения признака в точках, где пласт встречен скважиной (Р_гi). Затем по формуле 2.80 рассчитывается систематическая составляющая, а по формуле 2.79 — свободные от нее разности R_pi.

Погрешность скважинных измерений при этом равна


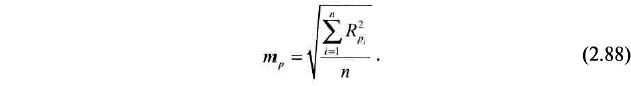
Однако, несмотря на простоту математической обработки, метод сложен в сборе данных, так как на практике сеть замеров в горных выработках не ориентирована на построение моделей и, следовательно, метод требует специальных долгосрочных наблюдений в шахтных условиях.

По результатам специальных исследований, проведенных с использованием разработанного метода и материалов горных работ шахт и разрезов Кузбасса, средние случайные погрешности скважинных определений составляют для:

• мощности пласта (по данным каротажа) — 15 см;
• пластовой зольности — 3 %
• зольности чистых угольных пачек — 2%;
• влаги — 2 %;
• выхода летучих — 2 %;
• пластометрического показателя X — 4 мм;
• пластометрического показателя Y — 2 мм;
• теплоты сгорания — 50 ккал/кг.

Исследования также показывают, что погрешность определения зольности практически не зависит от линейного выхода керна при диапазоне его изменения от 30 до 90 % [28]. Хотя считается, что его выход существенно влияет на представительность керновых проб, прежде всего при оценке зольности. Таким образом, ни высокая (выход керна более 70 %), ни средняя (от 50 до 70 %), ни даже низкая (от 30 до 50 %) представительность проб не является достаточным основанием для их отбраковки.
Оценка точности скважинных измерений мощности может выполняться и без привлечения данных горных работ, только по геологоразведочным данным.

В настоящее время мощность пласта определяется дважды: по каротажу (m_к) и по бурению (m_б). Разность R_m между получаемыми результатами измерений целиком обусловлена их погрешностями и, следовательно, несет информацию о них. Ее расшифровка возможна только на основе соответствующих гипотез о характере влияния ошибок.

В результате анализа литературных источников (работы А. А. Бойченко, В. А. Букринского, К. В. Гаврилина, В. И. Докиенко, Д. П. Жижина, Ю. М. Игнатова, В. С. Огаркова, Л. М. Печенкиной, С. Ф. Трофимова, Л. А. Шпеталенко) можно предположить, что случайные ошибки бурения зависят от величины пересекаемой мощности, а случайные ошибки каротажа не зависят от нее. Кроме того, для бурения характерна систематическая погрешность измерений, практически отсутствующая у каротажа. Специальные исследования, проведенные по методике А. И. Орлова [29], показали, что в пределах сопоставлений по отдельному пласту отсутствует статистически надежная связь между значениями систематических ошибок и величинами мощностей пласта. Данное обстоятельство имеет достаточно ясную физическую природу, рассмотренную в работах Г. М. Костоманова [23] и Ю. В. Буцика [6]. Поэтому, имея набор из n сопоставлений данных буровых и каротажных измерений, можно определять систематическую погрешность бурения с по формуле:


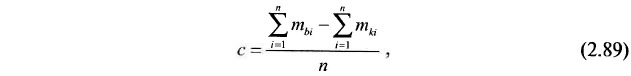
где m_бi и m_кi — мощность пласта по данным бурения и каротажа для i-ro пластоподсечения.

В ходе экспериментальных работ было установлено также, что линейная зависимость погрешности бурения от мощности пересекаемого пласта правомерна далеко не во всех случаях, на что впервые обратил внимание В. И. Докиенко [15]. Данное явление хорошо иллюстрируется рис. 2.75,а, на котором приведена экспериментальная зависимость между разностями R_m и мощностями пласта. Поэтому в теоретическую модель разности данных бурения и каротажа был введен специальный дополнительный коэффициент А.

Исходя из принятых гипотез и теории ошибок измерений, можно записать:


где R_mi = m_кi — m_бi + с (необходимость определения и учета систематической погрешности с устанавливается с помощью вышеописанной методики, использующей коэффициент конкордации);
k — случайная погрешность определения мощности по данным каротажа;
b — случайная относительная погрешность определения мощности по данным бурения;
m_ui — «истинная» мощность пласта.
Поскольку значение m_ui неизвестно, то с достаточной для практических целей точностью можно положить ее равной мощности по каротажу m_кi.

Таким образом, имея n сопоставлений, можно записать систему уравнений:


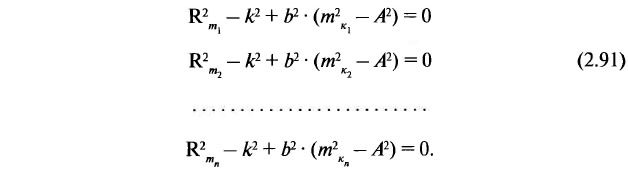
Непосредственное решение этой системы методом наименьших квадратов, в связи с формой участия в ней неизвестного коэффициента А, невозможно. Однако устанавливается, что:


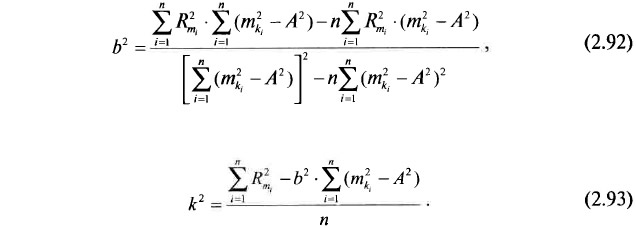
Процесс решения системы 2.91 заключается в том, чтобы путем перебора возможных величин А найти среди них такое, которое при вычислении погрешностей b и k по формулам 2.92 и 2.93 обеспечит минимальное значение суммы [εε] (что отвечает принципу аппроксимации по минимуму наименьших квадратов):


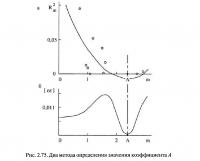
Наиболее просто данный подход реализуется на ЭВМ (перебор А начинается с А = 0 и завершается после нахождения первого минимума зависимости [εε] = f(А) — рис. 2.75, б).

При ручном варианте нахождения погрешностей целесообразно производить построение параболической зависимости, связывающей квадраты R²_mi (функция) и мощности пласта m_кi (аргумент) и имеющей экстремум при текущей мощности, равной А. Поэтому определение коэффициента А может быть осуществлено по формуле 2.95.

На рис. 2.75 приведены построенные по материалам шахты «Чертинская», совмещенные графики зависимости R²_mi. от мощности пласта m_кi (рис. 2.75,а) и [εε] от задаваемого значения А (рис. 2.75, б). Из рисунка следует полное совпадение значений А, независимо полученных двумя рассмотренными методами.


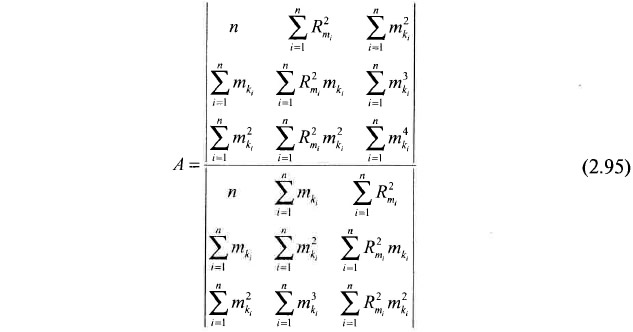
Проверка данного обстоятельства по 17 различным массивам сопоставлений подтвердила полученный результат: максимальное расхождение в значениях коэффициентов И составило всего 1 см.

Отметим, что в случае если в массиве сопоставлений преобладают мощности ниже А, то при квадрате погрешности бурения появляется знак «минус», т. е. погрешность мнима. Это вполне естественно, т. к. случайная абсолютная погрешность бурения в этом случае положительна:


где i — мнимая единица.

Исследование точности метода произведено на основе сравнения значений погрешностей, полученных с его помощью и на основе сравнения данных разведки и эксплуатации (таблица 2.28).


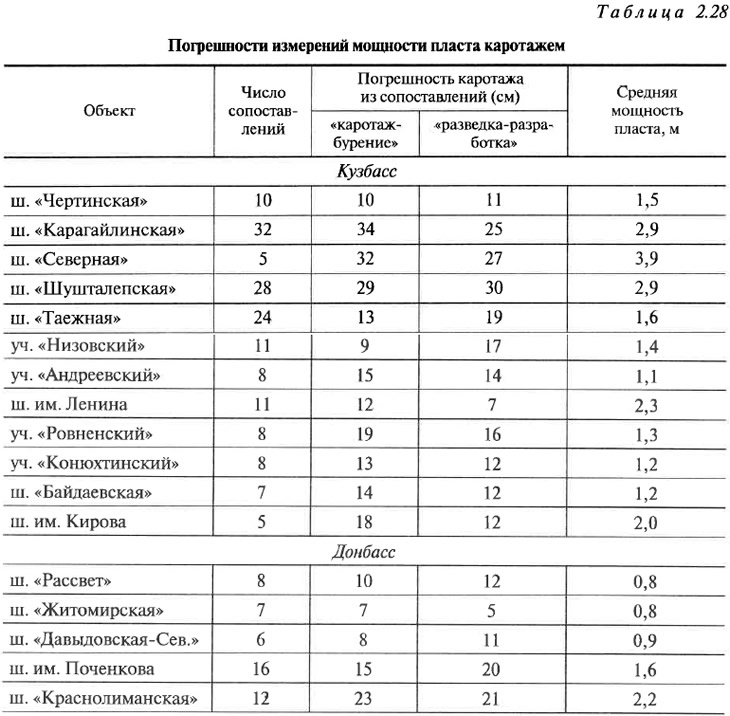
Поскольку в настоящее время мощности пластов принимаются практически только по данным каротажа, то в таблице приведено только сравнение погрешностей данного метода измерений (сравнение погрешностей бурения полностью приведено в работе [41]).

Как следует из таблицы 2.28, метод, основанный только на сравнении данных каротажа и бурения, дает достаточно надежные оценки погрешностей даже при незначительном количестве сопоставлений.