Выделение аномальных замеров мощностей пластов и показателей качества угля с помощью уравнивания

Задача выделения аномальных (ураганных) замеров является одной из окончательно не решенных проблем определения количества запасов и геометризации скрытых топографических поверхностей. Ошибочное выделение таких замеров приводит как к завышению, так и к занижению подсчетных значений мощностей пласта, зольности углей, содержания в них полезных и вредных компонентов и т. д., т. е. к внесению дополнительных погрешностей в оценку количества полезного ископаемого, ожидаемых концентраций токсичных и полезных компонентов. Кроме того, как уже отмечалось выше, выявление действительно аномальных замеров является необходимым этапом геометризации угольных пластов и оценки ее ожидаемой достоверности. Таким образом, выделение аномальных замеров преследует две различные цели:

• обеспечение получения надежной величины среднего значения признака;
• обеспечение построения надежной модели характера размещения значения признака в пространстве недр.

Практически все известные методы (количество которых уже превысило четыре десятка [19]) ориентируются на решение задачи определения средних содержаний компонентов рудных и россыпных месторождений по малому числу производимых определений. В силу того, что в этих условиях пространственные точки опробования являются геометрически независимыми, основные методы отбраковки справедливо не учитывают места размещения проб. Однако данное допущение применительно к анализу размещения мощностей и основных показателей качества углей является некорректным. К угольным месторождениям в наибольшей степени может быть применена идея В. М. Крейтера (1961) о том, что «...никаких исключительных («ураганных») проб вообще не существует и само понятие «ураганная проба» — исторический пережиток. Только несовершенство наших приемов опробования (добавим — и геометризации. — С. Ш.) вынуждает прибегать к искусственным приемам — заменять всевозможными путями исключительные пробы».

Поскольку при анализе материалов наиболее значимой задачей является выделение нехарактерных (аномальных) с позиции геометрического моделирования размещения признака, то их выделение не может игнорировать геометрию размещения проб и точек измерений.


Метод уравнивания нерегулярных цифровых моделей обеспечивает вполне корректное решение этой задачи. Как уже отмечалось, поправка к значению признака зависит от технических ошибок измерений и погрешностей интерполирования. Следовательно, если значение поправки резко выделяется по своей величине (см., например, рис. 3.5), то необходимо сделать вывод: либо признак определен по данному замеру с существенной ошибкой (в этом случае замер должен быть исключен из рассмотрения), либо в окрестности данной скважины имеет место резкое изменение характера поведения изучаемого признака (замер необходимо использовать при производстве оценки возможной точности геометризации).

Поэтому данный метод выделения ураганных замеров автоматически учитывает не только результат произведенного замера, но и его пространственное положение. В качестве примера в таблице 3.3 приведены значения поправок к практически одинаковым по величине мощностям (от 0,96 до 1,03 м), измеренным в скважинах, пробуренных по угольному пласту Семеновскому (участок «Ровненский» Кемеровского района Кузбасса). Она наглядно демонстрирует, как изменяется степень аномальности одного и того же значения мощности в зависимости от места расположения точки ее измерения.


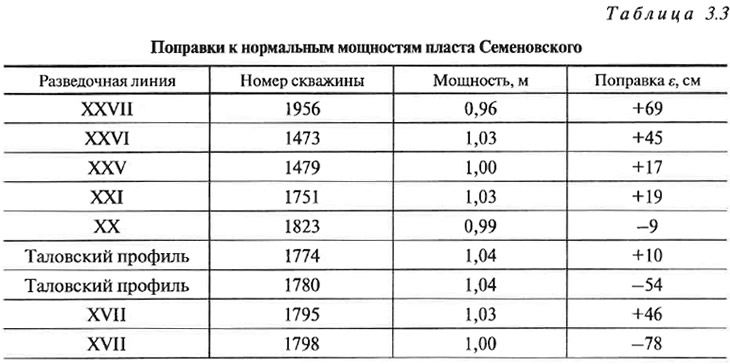
Значение каждой отдельной поправки определяется одновременно всеми значениями признака по всему рассматриваемому участку и плоскими координатами точек замера. Так, каждая поправка, приведенная на упомянутых фрагментах сети, есть функция от 228 (рис. 3.5, а) и 273 (рис. 3.5, б) факторов. Этим обеспечивается глубина анализа. Напомним, что человек в состоянии анализировать одновременно не более 7 ±2 факторов.


Выделение аномалий может быть осуществлено двумя путями.

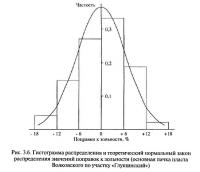
Первый путь состоит в отбраковке замеров по уровню значений поправок [44]. Предпосылками к его применению является зависимость величин поправок от значений определяемого признака и местоположения места замеров. Кроме того, исходя из методологии процесса уравнивания, поправки к измеряемым величинам должны распределяться по закону, близкому к нормальному, а их среднее арифметическое значение должно быть равно нулю (что подтверждается и экспериментальными исследованиями — например, рис. 3.6).

Поэтому признаком аномальности i-го замера при рассматриваемом подходе является выполнение условия:


где t — квантиль нормального закона распределения;
σ_ε — среднеквадратическое значение поправки, определяемое по формуле


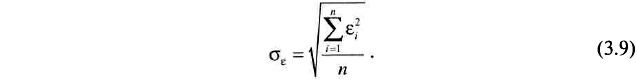
Практический опыт показывает, что в большинстве случаев целесообразно принимать t =1,8, что соответствует 7 %-й доли аномальных замеров (программа «LUR» обеспечивает производство расчетов при уровнях аномальности в 5, 7, 10, 12, 15, 17 и 20 %). Несмотря на то, что данный подход ориентирован на выявление аномальных замеров с позиции последующей геометризации, он может с успехом использоваться и при подсчете среднего значения признака, т. е. при подсчете запасов [44]. Оценка работоспособности метода, в плане его использования в указанном направлении, выполнена по результатам многовариантного разрежения разведочной сети по россыпному месторождению золота (опробованного по сети 5х5 м). В качестве интегральных показателей качества метода использовались общепринятые характеристики [19]:

• отношение числа случаев эффективной работы метода (когда в результате его применения среднее значение признака изменяется более чем на 5 % и приближается к истинному) к числу случаев дефектной (когда среднее значение признака изменяется более чем на 5 %, но отдаляется от истинного);
• процент случаев пропуска (нереагирования) больших (более +20 %) исходных положительных погрешностей.

Для рассматриваемого метода они составили соответственно 1,53 и 13 %. Лучший из известных методов (упрощенный метод П. Л. Каллистова) имеет значительно худшие показатели: 1,00 и 33 %. Являясь эффективным при подсчете запасов высокоизменчивых россыпных месторождений, метод должен являться таковым и при оценке ряда характеристик угольных. Тем не менее несколько позже в работе будет рассмотрен еще более результативный метод выделения ураганных замеров в ходе определения средних значений признаков в заданных контурах, работоспособность которого для условий россыпных и угольных месторождений доказана экспериментально.

Вторым подходом к поиску аномальных замеров является метод анализа приращений поправок. Его основная идея состоит в выделении нехарактерных замеров не по самим значениям поправок, а по степени их отличия от поправок в соседних точках измерений.

Сущность подхода разберем на фактическом примере — фрагменте разведочной сети по изучению сернистости угля (рис. 3.7).

Во-первых, на плане выделяются пары соседних замеров (практически ими будут являться стороны и диагонали выделенных оценочных четырехугольных блоков).

Во-вторых, оформляется таблица 3.4, в которую для каждого i-го замера сети выписываются все исходящие из него направления.


В-третьих, для каждого направления определяется взятая по абсолютной величине разность поправок. Затем на первом этапе произвольно задается критический уровень приращений U_к (1,00 % в табл. 3.4.). Разности поправок, превышающие U_к, маркируются (в табл. 3.4 они выделены жирным шрифтом).


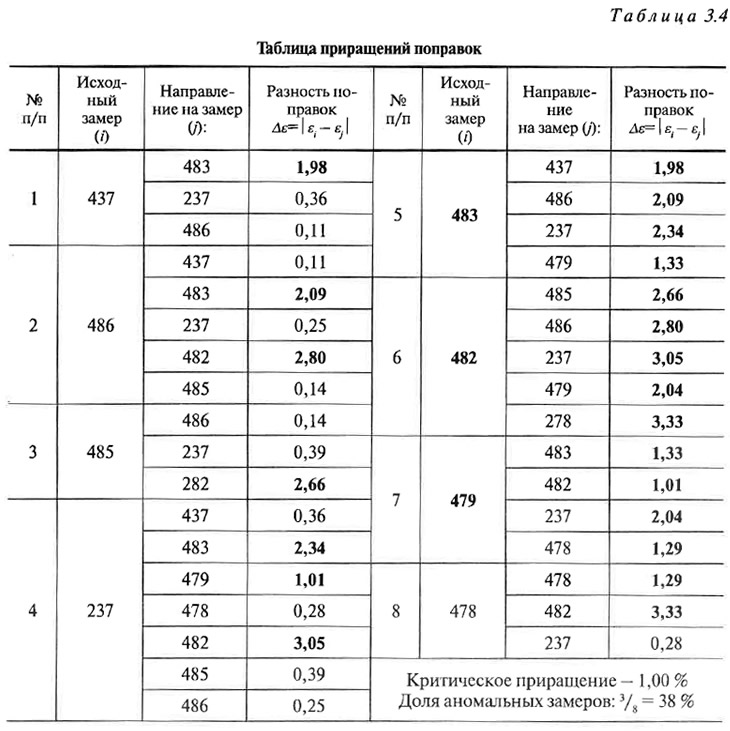
Анализируя таблицу, легко заметить, что три скважины (483,482 и 479) из восьми полностью отделены от соседних на величины критических приращений поправок и могут, следовательно, рассматриваться как аномальные. Доля аномальных замеров в массиве составляет:


где n — количество аномальных замеров;
N — общее количество замеров.

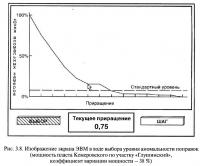
Поиск наиболее вероятного значения U_к осуществляется на основе построения и анализа зависимости вида U_к = f(D_a). На рис. 3.8 приведена копия экрана ЭВМ при работе в программе «LUR» с изображением указанной экспериментальной зависимости. Показанный на рисунке стандартный уровень соответствует 7%-му уровню аномальности первого описанного метода анализа.

При наличии нехарактерных (в геометрическом плане) замеров функция U_к = f(D_a) имеет своеобразную «ступеньку», протяженность которой зависит от «яркости» проявления аномальности на фоне общей изменчивости признака. Например, на рис. 3.9 эта ступенька выражена значительно более четко, чем на рис. 3.8. Соответствующее появлению «ступеньки» (т. е. участка устойчивых решений) значение критического приращения принимается за окончательное, и по его уровню выделяются аномальные замеры.

Оба описанных подхода дают в основном близкие результаты. Незначительные различия возникают лишь при наличии по участку аномальных зон (см. следующий параграф). Поэтому при анализе данных одновременно используются оба метода. При этом к аномальным относятся замеры, признанные таковыми хотя бы одним из методов.

При выполнении оценки точности геометризации данные по всем аномальным замерам подвергаются анализу на предмет подтверждения надежности произведенных в них измерений (методика выполнения которого была описана ранее). Если измерения недостоверны, то они исключаются из обработки, а если достоверны, то используются в нем, невзирая на уровень их аномальности. Отметим, что заведомо ошибочные замеры есть смысл сразу исключать из рассмотрения и не анализировать с помощью уравнивания.