Минералы шпинель и хризоберилл

Группа шпинели. Минералы этой группы представляют собой двойные окислы с общей формулой R⁺²O·R⁺³₂O₃ или R⁺²R⁺³₂O₄. Двухвалентные металлы могут быть представлены Mg, Fe⁺², Zn или Mn, а трехвалентные Al, Fe⁺³, Mn⁺³ или Cr⁺³. Много минералов группы найдено в природе, а еще больше получено искусственно. Все они относятся к кубической сингонии и обычно кристаллизуются в виде октаэдров или ромбододекаэдров. Представители группы, обнаруженные в природе, разделяются на три серии.


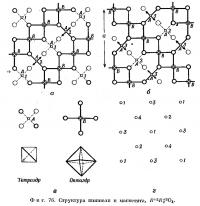
Первое исследование структуры шпинели было выполнено Брэггом (W. Н. Bragg, 1915) и Нисикавой (Nishikava, 1915). Структурный мотив шпинели довольно прост, но (как и для многих кубических кристаллов) изобразить структуру шпинели схематически трудно. Расположение атомов кислорода приближается к плотнейшей кубической упаковке. На фиг. 76, а и 76, б два слоя плотнейшей упаковки спроектированы на грань куба. Атомы A размещены в тетраэдрах из четырех атомов кислорода, а атомы B — в октаэдрах из шести атомов кислорода (фиг. 76, в). Эту же структуру можно изобразить в виде серии слоев (фиг. 76). В нижнем слое (фиг. 76, а) диагональная цепочка из B-октаэдров соединена A-тетраэдрами, которые располагаются попеременно выше и ниже атомов кислорода, обозначенных жирной линией. В следующем слое (фиг. 76, б) направление цепочек перпендикулярно предыдущему. Элементарная ячейка охватывает четыре таких слоя. На фиг. 76, г отмечены высоты атомов металла А. Видно, что они располагаются так же, как атомы углерода в алмазе. Каждый атом кислорода связан с одним атомом А и тремя атомами В. Структура построена из тетраэдров и октаэдров, и каждый атом кислорода принадлежит одному тетраэдру и трем октаэдрам.

В табл. 3 приведены константы решетки а и полученные по рентгеновским данным плотности ρ для нескольких синтетических шпинелей, измеренных Холгерсоном (Holgersson, 1927).



Структура шпинели относится к числу первых структур, исследованных с помощью рентгеновского анализа. Она казалась абсолютно четкой, однако более поздние работы Ринне (Rinne, 1928), Барта и Позняка (Barth, Posnjak, 1931), а также Махачки (Machatschki, 1931, 1932) обнаружили непредвиденные осложнения.

Поскольку содержание элементарной ячейки может быть выражено в общем виде как 8(XY₂O₄), представляется возможным разместить атомы X в восьми тетраздрах, а атомы У в шестнадцати октаэдрах. Барт и Позняк показали, что такое размещение не всегда правильно. Они разделили шпинели на два типа на основании рентгеновских данных:


к первому типу они отнесли ZnAl₂O₄, NiAl₂O₄, CoAl₂O₄, FeAl₂O₄ и MnAl₂O₄, а ко второму типу Fe⁺³MgFe⁺³O₄, GaMgGaO₄, InMgInO₄, MgTiMgO₄, Fe⁺²TiFe⁺²O₄ и ZnSnZnO₄.

Дунитц и Оргел (Dunitz, Orgel, 1957) изучали распределение атомов металла между тетраэдрическими и октаэдрическими положениями на основании теории кристаллического поля. Их теоретические прогнозы хорошо согласуются с экспериментальными данными. Они подсчитали разницу в энергиях, связанную с различным распределением электронов в ионе в зависимости от того, окружен ион электростатическим полем тетраэдра или октаэдра. В настоящей работе эта теория не рассматривается, однако о ее выводах следует кратко упомянуть. Избыток энергии устойчивости октаэдра, который и обусловливает октаэдрическое положение иона, понижается от иона к иону в следующем порядке: Сг⁺³, Mn⁺³, Ni⁺², Cu⁺², V⁺³, Co⁺², Ti⁺³, Fe⁺², Fe⁺³ и Mn⁺². Указанную последовательность следует рассматривать в связи с экспериментальными данными распределения катионов в шпинелях, приведенными в табл. 4. Цифрой 0 обозначена нормальная структура, в которой все двухвалентные ионы находятся в тетраэдрах, а цифрой 1 обозначена структура, в которой все двухвалентные ионы находятся в октаэдрах.



Поскольку хром является наиболее подходящим атомом для размещения в октаэдрах, следует ожидать, что все хромиты характеризуются нормальной структурой. Это подтверждается экспериментальными данными. Для Fe⁺³ и Mn⁺² указанная разность энергий исчезающе мала, следовательно, двухвалентный ион в ферритах занимает преимущественно октаэдрические положения, так-как Fe⁺³ размещается по тетраэдрам и октаэдрам структуры. Исключение представляет Mn⁺²Fe⁺³₂O₄, в котором электростатическая энергия решетки (константа Маделунга) обусловливает, по-видимому, нормальный тип решетки. Все алюминаты характеризуются нормальным типом решетки (включая типичную шпинель, MgAl₂O₄), за исключением Ni⁺²Al₂O₄. В этом соединении, согласно расчетам Дунитца и Оргела, энергия поля и энергия решетки почти точно сбалансированы. Цифра 0,76 указывает на почти беспорядочное распределение ионов между всеми возможными положениями. Следует отметить, что магнетит, FeFe₂O₄, представляет собой обращенную шпинель. Кубические решетки таких «шпинелей», как CuFe₂O₄, СиСг₂O₄, MnMn₂O₄ и ZnMn₂O₄, искажены до тетрагональных с отношением с/а, несколько превышающим единицу, в соответствии с характеристиками ионов Cu⁺² и Mn⁺³, отмеченными в гл. 2.

Другая интересная особенность структуры шпинели состоит в том, что в ней очень широко может меняться отношение А — В (Rinne, 1928). Идеальная шпинель имеет формулу MgO·Al₂O₃, но можно синтезировать шпинели состава MgO·nAl₂O₃, в которых n во много раз больше единицы. Это находится в соответствии с тем фактом, что γ-Al₂O₃ и γ-Fe₂O₃, которые могут рассматриваться в качестве крайних членов, имеют структуру типа шпинели.

Хризоберилл, BeAl₂O₄. Хотя формулы хризоберилла и шпинели сходны, их структуры различны. Структура хризоберилла была расшифрована Брэггом и Брауном (Bragg, Brown, 1926), а позднее уточнена Фаррелом, Фангом и Ньюнхемом (Farrell, Fang, Newnham, 1963).


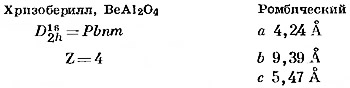
На фиг. 71 изображена идеализированная структура хризоберилла, что позволяет более наглядно показать характер упаковки атомов. Атомы кислорода приблизительно находятся в положениях гексагональной плотнейшей упаковки, где два слоя, перпендикулярные оси а, повторяются через каждые 4,24 Å. Эти два слоя изображены на фиг. 71. При наложении их друг па друга хорошо видно, что каждый атом Be занимает положение между четырьмя атомами О, а каждый атом Al между шестью атомами О. Хризоберилл очень часто образует двойники по (031) с псевдогексагональной симметрией, подобно арагониту (СаСO₃) и арканиту (K₂SO₄). Плотнейшая гексагональная упаковка атомов кислорода обусловливает псевдогексагональное отношение осей b и c. Давно установленное морфологическое подобие хризоберилла и оливина, Mg₂SiO₄, объясняется подобием их структур. При сравнении фиг. 71 и фиг. 121, а видно, что Be и Si, Al и Mg занимают аналогичные положения в обеих структурах.