Математические модели прогнозирования показателей разработки горизонтальными скважинами

2.7.1. Обзор исследований гидродинамики притока жидкости к горизонтальным и многозабойным скважинам

Теоретические исследования И.А. Чарного и А. М. Пирвердяна [177, 233] посвящены задачам притока жидкости к ГС бесконечной длины в пластах конечной толщины. Применение полученных решений для задач притока к ГС конечной длины приводит к заниженным результатам, причем ошибка при разной длине скважин и толщине пласта не поддается строгому определению. Работы П.А. Полубариновой-Кочиной [178] применимы, когда толщина пласта превосходит длину ГС. В случае, когда толщина пласта соизмерима с длиной ГС, решения имеют значительные погрешности. В.П. Меркуловым [135, 137] получены полуэмпирические формулы расчета дебитов скважин, которые имеют определенные пределы применимости. Результаты теоретических исследований М.Л. Сургучева и В.П. Меркулова [136] справедливы для наклонных скважин в слоистом пласте и имеют хорошее совпадение с данными экспериментов на электролитической модели. В 60-х годах во ВНИИ были проведены работы по созданию теоретических основ разработки нефтяных месторождений ГС и МГС. В.П. Пилатовский [175] предложил общую гидродинамическую теорию притока к ГС ограниченной протяжённости. В.П. Табаков рассмотрел установившийся приток жидкости к одиночным наклонным многозабойным скважинам и скважинам сложного профиля [211—216]. Расчёт взаимодействия МГС предложен Ю.П. Борисовым и В.П. Табаковым. Расчёт дебитов скважин был проведён в предположении постоянного расхода жидкости по всей длине ствола скважины, что является не вполне правомерным. Большой интерес представляет работа В.И. Шурова [245], выполненная на электролитической модели. Результаты этих экспериментов сведены в таблицы, на основе которых построены графические зависимости. Задачи притока к ГС рассматривались в работах многих российских и американских исследователей [145, 146, 165, 235, 237, 255, 275 и др.]. Следует отметить, что в точной постановке задачи притока к ГС (задачи Гильберта — Рима-на) аналитического решения не получено. Оценка эффективности горизонтальных скважин в сравнении с вертикальными в представленных работах не достаточно достоверна, так как сравнивались дебиты скважин при несопоставимости областей дренирования.

2.7.2. Постановка задачи математического моделирования притока жидкости к горизонтальным стволам скважин

Впервые такая постановка задачи приведена в работах Н.В. Ювченко [159 и др.]. Результаты этих работ и полученные на их основе выводы, приведенные в п. 2.7.3—2.7.5, 2.9, были использованы нами при выборе опытных участков и определении конструкции при строительстве ГС. Технологические показатели разработки опытных участков обосновывались, исходя из результатов численного моделирования по методике, приведенной в п. 2.8.


Методы решения этих уравнений подробно рассмотрены в работе [156].

Далее будем рассматривать интегральное уравнение следующего вида


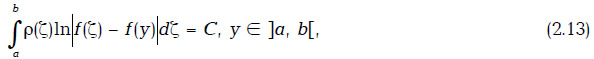
где С — некоторая константа.

Замечания к уравнению (2.11): если f(x) — строго монотонная и дифференцируемая функция на отрезке [a, b], то решение уравнения (2.13) существует единственно и имеет вид:


где C₁ — некоторая константа.


Справедливость замечания к (2.11) следует из данных работы [156].

2.7.3. Моделирование притока к горизонтальным и многозабойным скважинам на плоскости

Рассмотрим задачи притока к ГС и МГС на плоскости. Ценность данных задач состоит в том, что они имеют точные аналитические решения. Для некоторых из них решения найдены впервые.

А. Рассмотрим случай, когда ГС определяется множеством —1≤x≤1, y=0 на плоскости 0_xy.

Фундаментальное решение уравнения Лапласа для него имеет вид


а соответствующее интегральное уравнение запишем следующим образом:


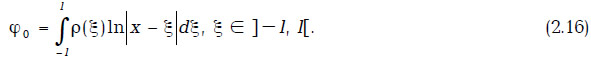
В газовой динамике это уравнение теории крыла самолёта, решением которого является функция [156]


Поле потенциалов скоростей фильтрации ГС определяется функцией


где A, B — const, а S является положительным корнем уравнения



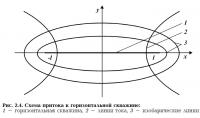
Отметим, что (2.19) описывает изобарические линии притока ГС, S — параметр изобары.

Линии тока данного течения определяются следующим уравнением:


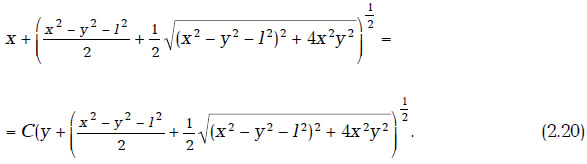
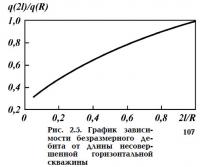
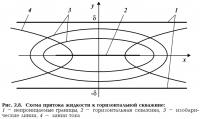
Схема притока к ГС поясняется на рис. 2.4. На рис. 2.5 показано, как зависит дебит от длины несовершенной ГС.

Рис. 2.4. Схема притока к горизонтальной скважине

Рис. 2.5. График зависимости безразмерного дебита от длины горизонтальной скважины

Вычислим дебит ГС при условии, что потенциал скорости фильтрации на скважине равен φ_с, контуром питания является изобарическая линия S=R², потенциал на контуре питания равен φ₁. В этом случае потенциал, создаваемый ГС, примет вид


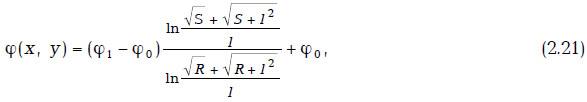
где S — положительный корень уравнения (2.21).


Тогда дебит ГС равен


где С — любая изобарическая линия, определяемая уравнением (2.21); δφ/δn — нормальная производная, n — вектор нормали к кривой С.

Вычисляя последний интеграл, имеем


Б. Пусть на плоскости 0_xy между прямыми у=δ, у=—δ расположена ГС с координатами концов (0, l) и (0, l). В работе [218] показано, что потенциал точечного источника, расположенного в точке (0, η) имеет вид


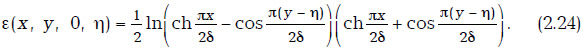
Интегральное уравнение в данном случае выглядит как



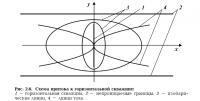
Отметим, что (2.30) — уравнение изобарических линий данного течения, S — параметр изобары. Схема притока к ГС приведена на рис. 2.6.

Пусть на скважине задан потенциал скоростей фильтрации φ₀, а на контуре питания х = R — потенциал φ₁. В этом случае


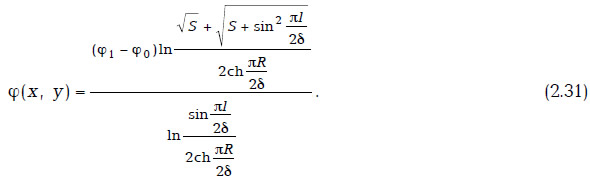
Тогда дебит ГС равен


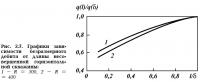
Зависимость безразмерного дебита от величины i/6 приведена на рис. 2.7.

В. Рассмотрим задачу с распределением расхода жидкости по длине ГС, расположенной между двумя непроводящими прямыми у=δ и у=-δ; скважина определена координатами концов (-l, 0) и (0, l). В этом случае задача о распределении расхода жидкости по длине ГС сводится к решению интегрального уравнения



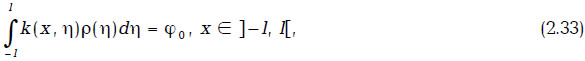
Уравнение (2.37) описывает изобарические линии данного течения, S — параметр изобары.

Схема притока к ГС приведена на рис. 2.8.

Пусть на скважине задано давление Р₀, на контуре питания х = R — давление Р₁, тогда дебит ГС равен


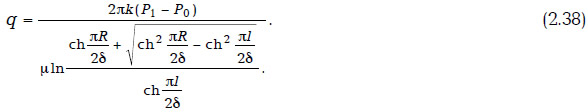
Г. Пусть на плоскости 0_xy между прямыми у=δ, у=-δ расположена ГС с координатами (0, l₁) и (0, -l₂). Соответствующее интегральное уравнение имеет вид


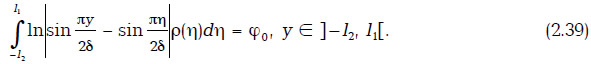
Решая уравнение (2.39), найдем


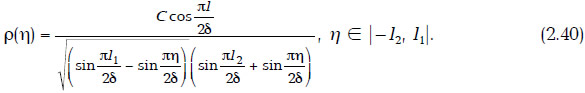
Д. Рассмотрим приток к многозабойной горизонтальной скважине (МГС) на плоскости 0_xy. Скважину, имеющую n≥2 горизонтальных стволов, опишем в полярных координатах (ρ, φ) следующим образом:


где l — длина ствола.

Нетрудно догадаться, что потенциал, создаваемый многозабойной скважиной, равен


где S — положительный корень уравнения


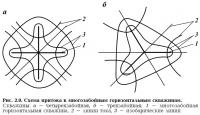
Заметим, что (2.43) — уравнение изобарических линий, S — параметр изобары. На рис. 2.9 приведена схема притока к многозабойным скважинам при n = 3, 4.

Пусть на стволах МГС задан потенциал скоростей фильтрации φ₀, на контуре питания (некоторая изобарическая линия R_n=S) — потенциал φ₁, тогда потенциал, создаваемый МГС, равен


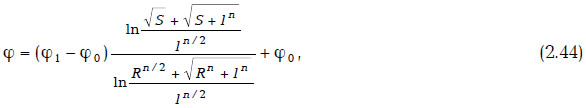
где S — положительный корень уравнения (2.43).

Дебит многозабойной горизонтальной скважины


Следует отметить, что в работе [43] приводится приближенная формула дебита МГС:


где коэффициент С зависит от числа стволов n. Но как видно из формулы (2.45), коэффициент С зависит от l, R и n. Поэтому нетрудно привести пример, когда формула (2.39) будет иметь значительную погрешность.

Зависимость безразмерного дебита МГС от величины 2l/R приведена на рис. 2.10.

Расчеты показывают, что при увеличении числа стволов, начиная с n=3, увеличение дебита незначительно. Отметим, что формула (2.38) при n=2 совпадает с формулой дебита горизонтальной скважины с длиной ствола 21.

2.7.4. Моделирование притока к одиночной горизонтальной скважине в пласте конечной толщины

До настоящего времени в литературе не приводится точных аналитических решений задач о притоке жидкости к горизонтальным и многозабойным скважинам в пласте конечной толщины. Имеются лишь приближенные формулы для расчета дебита ГС и МГС.

А. Для расчета дебита ГС в работе [43] используется метод фильтрационных сопротивлений Ю.П. Борисова [39]. Формула дебита ГС имеет следующий вид:


где 2l — длина ГС, R_к — радиус контура питания, r — радиус ГС.

Для оценки точности данной формулы были приведены результаты электростатического моделирования [245], которые показали приемлемую точность (2.47).

Более точная формула получена в [212]:


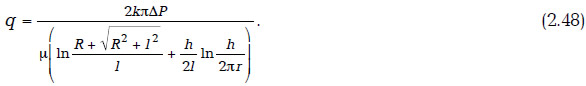
Б. Рассмотрим задачу о притоке к многозабойной горизонтальной скважине в пласте конечной толщины. В [43] приведена приближенная формула дебита МГС, которая выведена на основании формулы (2.46):


где величина x(n) определяется по табуляграмме и зависит только от числа символов. Ранее указывалось, что в общем случае, величина х зависит от n, l, R, поэтому эта формула может допускать значительные погрешности.

Для вычисления дебита многозабойной горизонтальной скважины воспользуемся формулой дебита МГС на плоскости (2.45) и методом фильтрационных сопротивлений. В этом случае выражение дебита многозабойной горизонтальной скважины в пласте конечной толщины примет вид


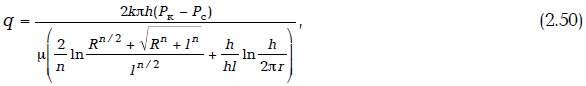
где n — число стволов, l — длина ствола.

Заметим, что при n = 2 имеем формулу для дебита ГС в пласте конечной толщины.

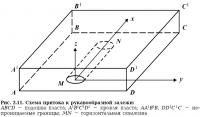
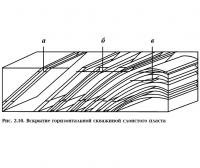
В. Пусть горизонтальная скважина расположена в рукавообразной залежи. Модель данного течения представлена на рис. 2.11.

Горизонтальная скважина, ось которой направлена вдоль потока, равноудалена от непроницаемых граней. Применяя теорию фильтрационных сопротивлений и используя соотношение (2.37), получим


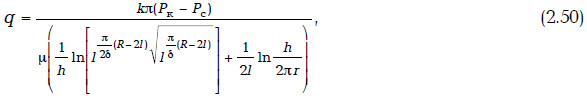
где δ — ширина потока, l — длина ГС.

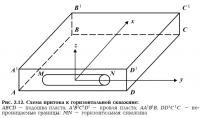
Г. Рассмотрим модель течения к горизонтальной скважине, схематично изображенной на рис. 2.12.

Скважина расположена в центре пласта и равноудалена от непроницаемых граней.

Дебит такой скважины


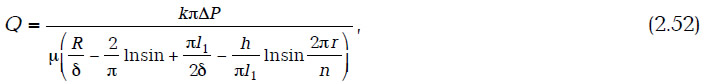
где 2l — длина ствола ГС; r — радиус ГС, 2δ — ширина потока. Отметим, что формула (2.37) выведена в предположении неравномерного расхода жидкости по длине ствола ГС. Расход жидкости по длине ствола определяется формулой


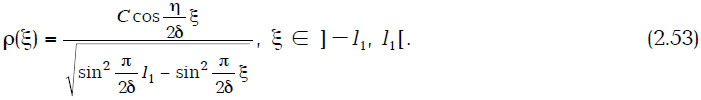
Таким образом, в данном разделе приведены точные аналитические решения задач притока к ГС и МГС на плоскости. Найдено распределение расхода жидкости по длине горизонтальной скважины. Заметим, что до настоящего времени при решении задач притока к ГС и МГС принималось предположение о равномерности расхода по длине скважины.

Результаты исследования используются при моделировании горизонтальной скважины в моделях многофазной фильтрации. Известно, что на расстоянии, равном двум толщинам однородного пласта, от горизонтальной скважины нормаль к фронту вытеснения направлена вдоль простирания пласта. В связи с этим для настройки моделей многофазной фильтрации в режиме поддержания пластового давления могут быть использованы уравнения изобарических линий рассмотренных здесь течений. Уточнены формулы дебитов ГС и МГС в пласте конечной толщины и получена формула для расчета ГС в рукавообразной залежи.

2.7.5. Зависимости дебита скважины от протяженности горизонтального ствола

При выборе систем разработки залежей нефти с применением ГС, одним из ключевых вопросов является обоснование оптимальной протяженности горизонтального ствола. Ниже рассмотрим влияние длины ГС на дебит скважин при однорядной и трехрядной схемах размещения, влияние протяженности горизонтального ствола на коэффициент извлечения нефти и другие вопросы выбора оптимальной длины ГС.

Линейная однорядная система размещения горизонтальных скважин

Для упрощения расчетов по определению показателей разработки при данной системе заводнения предполагается одновременный ввод всех скважин в эксплуатацию. Равномерна я сетка скважин по площади предопределяет равнодебитность элементов системы.

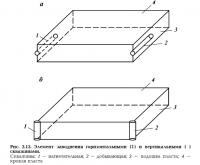
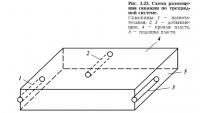
Однородный пласт. Для этого случая элемент системы заводнения представлен на рис. 2.13, а. Все грани параллелепипеда непроницаемы, скважины проходят по середине пласта. Дебит скважины, как отмечалось выше, для этого элемента определится формулой


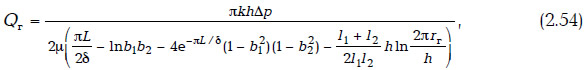
где L — расстояние между скважинами; δ — ширина потока; h — толщина пласта; Δр — депрессия; k/μ — подвижность; l_i — длина i-й скважины; r_r — радиус горизонтальной скважины;


В случае, когда горизонтальные скважины полностью вскрывают элемент заводнения, т.е. l=δ, формула (2.54) примет вид:


Для оценки эффективности данной системы размещения сравним ее с линейной системой заводнения вертикальными скважинами, элемент которой представлен на рис. 2.13, б.

Дебит вертикальной скважины


Введем соотношение производительности горизонтальной и вертикальной скважин:


В качестве базового варианта разработки выберем линейную систему размещения вертикальных скважин:

I — в рядах число горизонтальных скважин равно числу вертикальных скважин (N_г = N_в, расстояние между серединами ГС равно 2δ).

II — в рядах число горизонтальных скважин в два раза меньше числа вертикальных скважин (N_г = 1/2 N_в, расстояние между серединами ГС равно 4δ).

В обоих случаях расстояние между рядами скважин равно 2δ, длины стволов нагнетательных и добывающих скважин ГС равны.

На рис. 2.14 представлено отношение производительности ГС при l-м варианте размещения скважин к производительности ВС базисного варианта при δ = 150 и 300 м и h = 10 и 20 м в зависимости от величины 1/δ.

Рассмотрим случай, когда элемент заводнения полностью вскрывается ГС (l = δ), h = 10 м; тогда увеличение дебита составит: γ = 4,6 при δ = 150 м; γ = 5,1 при δ = 300 м.

На рис. 2.15 показана зависимость отношение производительности ГС второго варианта размещения (N_г = 1/2N_в) к производительности ВС базового варианта.

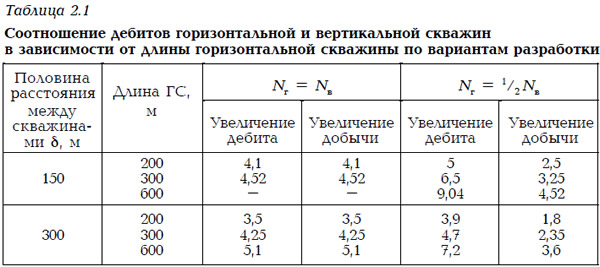
Положим h = 10 м и представим увеличение дебитов ГС и общей добычи по сравнению с базовым вариантом при δ = 150 и 300 м (таблица 2.1) в зависимости от ствола ГС. Из табл. 2.1 следует:

• сокращение числа ГС в рядах в 2 раза приводит к увеличению производительности ГС и уменьшению добычи в сравнении с вариантом N_г = N_в;
• эффективность ГС возрастает на более плотных сетках;
• влияние длины ствола ГС на производительность более существенна в случае N_г = 1/2N_в, чем при N_г = N_в.

На рис. 2.13, 2.14 видно, что с уменьшением толщины пласта h эффективность ГС возрастает.


Слоистый пласт. Предположим, что пласт толщиной h состоит из n пропластков равной толщины h/n и вскрывается горизонтальной скважиной, как показано на рис. 2.16, а, в.

В этом случае в каждом пропластке получаются одинаковые сетки горизонтальных скважин длиной 2l/n, где 2l — длина ГС, n — число пропластков.

Как и в случае однородного пласта, выберем базисный вариант разработки — линейную систему размещения вертикальных скважин (2δx2δ) и два варианта размещения ГС: первый с N_г = N_в и второй с N_г = 1/2N_в.

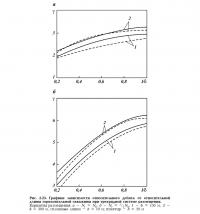
На рис. 2.17 и 2.18 представлено отношение производительности ГС к производительности ВС для слоистого пласта при h = 10 м; δ = 150 м, l = 150 и 300 м; n = 1, 2, 3, 4, 5.

С увеличением числа пропластков эффективность ГС уменьшается. Так при h = 10 м, δ = 150 м, l = 150 м дебиты горизонтальных скважин при первом варианте размещения больше дебитов вертикальных скважин в 4,5 раза (n=1); для h = 10 м, δ = 300 м, l = 150 м — в 3 раза (n=3).

Рис. 2.16. Вскрытие горизонтальной скважиной слоистого пласта

Рис. 2.17. Графики зависимости производительности от длины горизонтального ствола

Рис. 2.18. Графики зависимости производительности от длины горизонтального ствола

Однорядная система размещения горизонтальных скважин

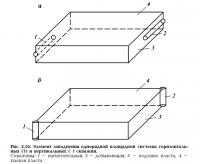
Элемент заводнения однорядной площадной системы размещения горизонтальных скважин представлен на рис. 2.19, а. Для оценки эффективности данной системы размещения скважин сравним ее с площадной системой заводнения вертикальными скважинами, элемент которой представлен на рис. 2.19, б.

В случае однородного пласта толщиной h дебит горизонтальной скважины, как отмечено выше, определяется формулой


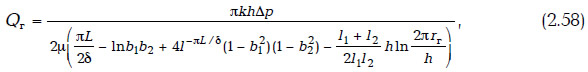
а дебит вертикальной скважины [159]:


Здесь обозначения такие же, как и в предыдущем разделе. Введем величину γ, определяющую отношение дебитов горизонтальных и вертикальных скважин. В качестве базового варианта разработки выберем площадную пятиточечную систему размещения вертикальных скважин. Рассмотрим, как и в предыдущем разделе, два варианта размещения горизонтальных скважин:

I — в рядах число горизонтальных скважин равно числу вертикальных скважин (Nг = N_в).

II — в рядах число горизонтальных скважин в 2 раза меньше числа вертикальных скважин (Nг = 1/2N_в).

На рис. 2.20 представлена зависимость величины γ от l/δ для второго варианта размещения ГС.

Для первого варианта размещения ГС зависимость практически такая же, как и в случае линейной системы размещения (см. рис. 2.15). На рис. 2.21 представлена зависимость γ от l для слоистого пласта.

Таким образом, выводы предыдущего раздела справедливы и в данном случае, т.е.:

• сокращение числа ГС в рядах в 2 раза приводит к увеличению производительности ГС и уменьшению добычи в сравнении с вариантом N_г = N_в;
• эффективность ГС возрастает при более плотных сетках скважин;
• влияние длины ствола ГС на производительность более существенна в случае N_г = 1/2N_в;
• для слоистого пласта с увеличением числа пропластков, эффективность ГС уменьшается.

Рис. 2.19. Элемент заводнения однорядной площадной системы скважин

Рис. 2.20. Графики зависимости производительности горизонтальных скважин

Рис. 2.21. Графики зависимости относительного дебита от длины горизонтального ствола

Трехрядная система размещения скважин

Рассмотрим трехрядную систему размещения горизонтальных скважин. Предполагаем, что в каждом ряду скважины находятся на одинаковом расстоянии друг от друга, забойные давления во всех скважинах одного ряда одинаковы, длина и радиусы горизонтальных скважин одинаковы, горизонтальные скважины проведены на одинаковом расстоянии от подошвы и кровли пласта. Элемент, удовлетворяющий поставленным условиям, представлен на рис. 2.22.

Тогда, исходя из данных работы [159], можно записать:



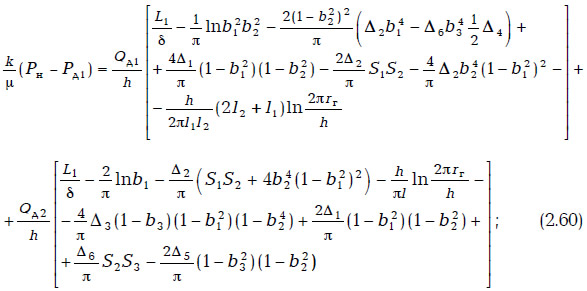
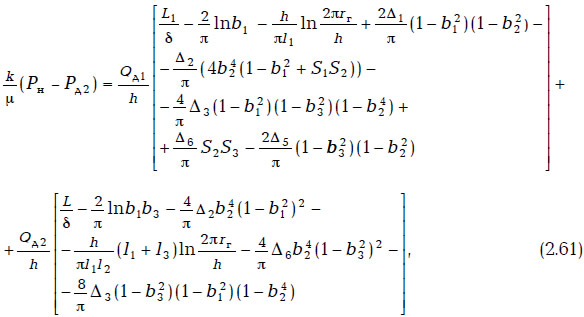
где P_н, Р_д1, Р_д2 — давление на нагнетательной и добывающих скважинах соответственно;
Q_д1, Q_д2 — дебиты добывающих скважин;
l₁ — расстояние между рядом нагнетательных и первым рядом добывающих скважин;
l_i — длина i-й скважины;
2δ — расстояние между скважинами в ряду;


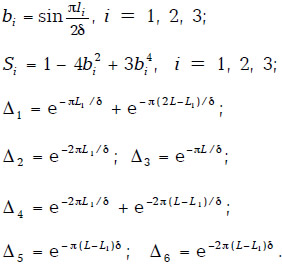
Как и в предыдущих разделах, для оценки эффективности данной системы размещения сравним ее с трехрядной системой размещения вертикальных скважин.

Введем отношение производительности нагнетательных скважин ГС к производительности нагнетательных ВС.


В качестве базового варианта выберем трехрядную систему размещения ГС (расстояние между рядами 2δ, между скважинами в рядах 2δ). Рассматриваем два варианта размещения горизонтальных скважин:

I — в рядах число горизонтальных скважин равно числу вертикальных скважин (N_г = N_в).

II — в рядах число горизонтальных скважин в два раза меньше числа вертикальных скважин (N_г = 1/2N_в).

Длины стволов нагнетательных и добывающих скважин равны, расстояние между ГС составляет 2δ.

Дополнительные условия: дебиты ГС первого и второго ряда равны Q_д1 = Q_д2 в уравнениях (2.60), (2.61); депрессия между нагнетательной скважиной и добывающей скважиной 2-го ряда одинакова во всех случаях.

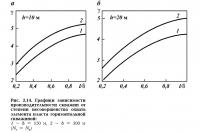
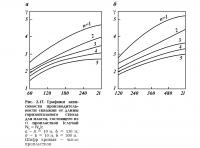
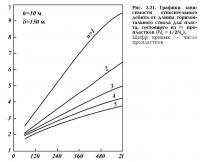
Результаты расчетов приведены на рис. 2.23, а, где представлено отношение производительности ГС для первого варианта размещения к производительности ВС при δ = 150 и 300 м, h = 10 и 20 м в зависимости от величины 1/δ. Рассмотрим случай, когда элемент полностью вскрывается ГС, h = 10 м; тогда увеличение дебитов ГС составит γ = 3,0 при δ = 150 м; γ = 3,5 при δ = 300 м.

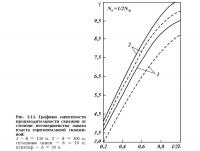
Результаты расчетов отношения производительности ГС для второго варианта размещения (N_г = 1/2N_в) к производительности ВС базисного варианта представлены на рис. 2.23, б. Далее положим h = 10 м и представим результаты расчетов увеличения дебитов ГС и общей добычи по сравнению с базисным вариантом при δ = 150 и 300 м в зависимости от длины ствола ГС (табл. 2.2).

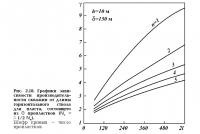
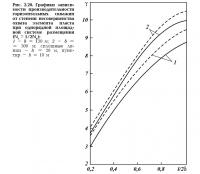
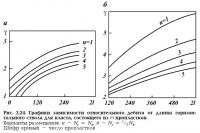
Результаты расчетов увеличения дебитов горизонтальных скважин в зависимости от длины горизонтального ствола для пласта, состоящего из n пропластков, приведены на рис. 2.24.


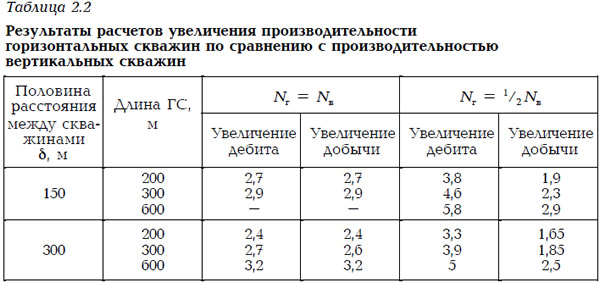
Анализ результатов расчетов показывает:

• эффективность ГС возрастает на более плотных сетках;
• эффективность ГС при трехрядной системе размещения ниже эффективности ГС при однорядной, площадной и линейной системах размещения;
• влияние длины ствола ГС на производительность более существенна в случае N_г = 1/2N_в, чем при N_г = N_в;
• сокращение числа ГС в рядах в 2 раза приводит к увеличению производительности ГС и уменьшению добычи в сравнении с вариантом N_г = N_в;
• с уменьшением толщины пласта эффективность ГС возрастает;
• с увеличением числа пропластков слоистого пласта эффективность ГС уменьшается.